题目内容
3.空间四边形ABCD中,M、G分别是BC、CD的中点,则$\overrightarrow{MG}$-$\overrightarrow{AB}$+$\overrightarrow{AD}$等于( )| A. | $\frac{3}{2}$$\overrightarrow{DB}$ | B. | 3$\overrightarrow{MG}$ | C. | 3$\overrightarrow{GM}$ | D. | 2$\overrightarrow{MG}$ |
分析 作图,从而化简$\overrightarrow{MG}$-$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{MG}$-($\overrightarrow{AB}$-$\overrightarrow{AD}$)=$\overrightarrow{MG}$-$\overrightarrow{DB}$=$\overrightarrow{MG}$-(-2$\overrightarrow{MG}$)=3$\overrightarrow{MG}$.
解答 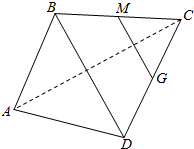 解:如图,
解:如图,
$\overrightarrow{MG}$-$\overrightarrow{AB}$+$\overrightarrow{AD}$
=$\overrightarrow{MG}$-($\overrightarrow{AB}$-$\overrightarrow{AD}$)
=$\overrightarrow{MG}$-$\overrightarrow{DB}$
=$\overrightarrow{MG}$-(-2$\overrightarrow{MG}$)
=3$\overrightarrow{MG}$,
故选B.
点评 本题考查了空间向量的加法运算,减法运算,数乘运算的综合应用.

练习册系列答案
相关题目
13.已知$sin\frac{α}{2}-cos\frac{α}{2}=-\frac{{\sqrt{2}}}{2}$,且cosα<0,则tanα=( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
18.己知α是第三象限角,且tanα=$\frac{5}{12}$,则cosα的值是( )
| A. | -$\frac{5}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
12.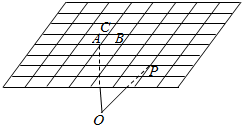 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )| A. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$+2$\overrightarrow{AC}$ | B. | $\overrightarrow{OA}$-3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | C. | $\overrightarrow{OA}$+3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | D. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$-3$\overrightarrow{AC}$ |
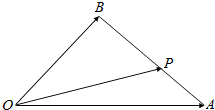 如图,在△AOB中,已知P为线段AB上的一点,且$\overrightarrow{BP}$=2$\overrightarrow{PA}$.
如图,在△AOB中,已知P为线段AB上的一点,且$\overrightarrow{BP}$=2$\overrightarrow{PA}$.