题目内容
17.求下列圆的方程:(1)已知点A(-4,-5),B(6,-1),以线段AB为直径的圆的方程.
(2)过两点C(-1,1)和D(1,3),圆心在x轴上的圆的标准方程.
分析 (1)由点A和点B的坐标,利用中点坐标公式求出线段AB的中点C的坐标,因为线段AB为所求圆的直径,所以求出的中点C的坐标即为圆心坐标,然后由圆心C的坐标和点A的坐标,利用两点间的距离公式求出|AC|的长即为圆的半径,根据圆心和半径写出圆的标准方程即可.
(2)设圆心坐标为C(a,0),根据A、B两点在圆上利用两点的距离公式建立关于a的方程,解出a值.从而算出圆C的圆心和半径,可得圆C的方程.
解答 解:(1)由中点坐标公式得线段AB的中点坐标为C(1,-3),即圆心的坐标为C(1,-3).
r=|AC|=$\sqrt{(1+4)^{2}+(-3+5)^{2}}$=$\sqrt{29}$,
故所求圆的方程为:(x-1)2+(y+3)2=29.
(2)设圆心坐标为C(a,0),
∵点A(-1,1)和B(1,3)在圆C上,
∴|CA|=|CB|,即$\sqrt{(a+1)^{2}+(0-1)^{2}}$=$\sqrt{(a-1)^{2}+(0-3)^{2}}$,
解之得a=2,可得圆心为C(2,0),
半径|CA|=$\sqrt{(2+1)^{2}+(0-1)^{2}}$=$\sqrt{10}$,
∴圆C的方程为(x-2)2+y2=10.
点评 本题的考点是圆的标准方程,考查学生灵活运用中点坐标公式及两点间的距离公式化简求值,求圆心坐标和半径是求圆的标准方程的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.在△ABC中,$\overrightarrow{AB}$=(2cosα,2sinα),$\overrightarrow{BC}$=(5cosβ,5sinβ),若$\overrightarrow{AB}$$•\overrightarrow{BC}$=-5,则|$\overrightarrow{AC}$|=( )
| A. | 4 | B. | $\sqrt{10}$ | C. | $\sqrt{19}$ | D. | 25 |
12.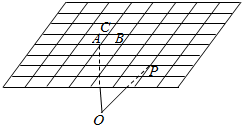 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )| A. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$+2$\overrightarrow{AC}$ | B. | $\overrightarrow{OA}$-3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | C. | $\overrightarrow{OA}$+3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | D. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$-3$\overrightarrow{AC}$ |