题目内容
7．已知f（x）=$\left\{\begin{array}{l}{{2}^{x-1}，x≤0}\\{f（x-1）-f（x-2），x＞0}\end{array}\right.$，则 f（2016）=$\frac{1}{2}$．分析 根据已知中函数的解析式，分析出f（x）是周期为6的周期函数，进而可得答案．
解答 解：∵当x＞0时，f（x）=f（x-1）-f（x-2），
f（x-1）=f（x-2）-f（x-3），
得出f（x）=-f（x-3），可得f（x+6）=f（x），所以周期是6．
所以f（2016）=f（336×6）=f（0），
=2 0-1=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查分段函数的应用，求函数值，要确定好自变量的取值或范围，再代入相应的解析式求得对应的函数值．分段函数分段处理，这是研究分段函数图象和性质最核心的理念
练习册系列答案
相关题目
17．不等式组$\left\{\begin{array}{l}y≥0\\ x+3y≤4\\ 3x+y≥4\end{array}\right.$，所表示的平面区域的面积等于（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{4}{3}$ | D． | $\frac{3}{4}$ |
18．己知α是第三象限角，且tanα=$\frac{5}{12}$，则cosα的值是（ ）
| A． | -$\frac{5}{13}$ | B． | $\frac{5}{13}$ | C． | $\frac{12}{13}$ | D． | -$\frac{12}{13}$ |
2．下列条件使M与A，B，C一定共面的是（ ）
| A． | $\overrightarrow{OM}$=2$\overrightarrow{OA}$-$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B． | $\overrightarrow{OM}$+$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$ | ||
| C． | $\overrightarrow{OM}$=$\frac{1}{5}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$ | D． | $\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=$\overrightarrow{0}$ |
12．
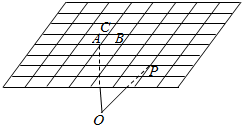如图所示，已知A，B，C三点不共线，P为一定点，O为平面ABC外任意一点，则下列能表示向量$\overrightarrow{OP}$的为（ ）
如图所示，已知A，B，C三点不共线，P为一定点，O为平面ABC外任意一点，则下列能表示向量$\overrightarrow{OP}$的为（ ）| A． | $\overrightarrow{OA}$+2$\overrightarrow{AB}$+2$\overrightarrow{AC}$ | B． | $\overrightarrow{OA}$-3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | C． | $\overrightarrow{OA}$+3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | D． | $\overrightarrow{OA}$+2$\overrightarrow{AB}$-3$\overrightarrow{AC}$ |