题目内容
2.函数y=$\frac{ln(x+1)}{{\sqrt{{3^x}-27}}}$的定义域为( )| A. | (-1,+∞) | B. | (-1,3) | C. | (3,+∞) | D. | [3,+∞) |
分析 由对数式的真数大于0,分母中根式内部的代数式大于0联立不等式组得答案.
解答 解:由$\left\{\begin{array}{l}{x+1>0}\\{{3}^{x}-27>0}\end{array}\right.$,解得x>3.
∴函数y=$\frac{ln(x+1)}{{\sqrt{{3^x}-27}}}$的定义域为(3,+∞).
故选:C.
点评 本题考查函数的定义域及其求法,考查了指数不等式的解法,是基础题.

练习册系列答案
相关题目
13.已知$sin\frac{α}{2}-cos\frac{α}{2}=-\frac{{\sqrt{2}}}{2}$,且cosα<0,则tanα=( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
17.不等式组$\left\{\begin{array}{l}y≥0\\ x+3y≤4\\ 3x+y≥4\end{array}\right.$,所表示的平面区域的面积等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
12.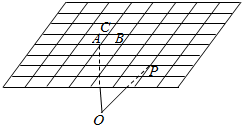 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )| A. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$+2$\overrightarrow{AC}$ | B. | $\overrightarrow{OA}$-3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | C. | $\overrightarrow{OA}$+3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | D. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$-3$\overrightarrow{AC}$ |
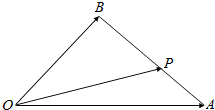 如图,在△AOB中,已知P为线段AB上的一点,且$\overrightarrow{BP}$=2$\overrightarrow{PA}$.
如图,在△AOB中,已知P为线段AB上的一点,且$\overrightarrow{BP}$=2$\overrightarrow{PA}$.