题目内容
抛物线的准线l的方程是y=l,且抛物线恒过点P(1,一1),则抛物线焦点弦PQ的另一个端点Q的轨迹方程是( )
| A、(x-1)2=-8(y-1) |
| B、(x一1)2=-8(y-1)(x≠1) |
| C、(y一1)2=8(x一1) |
| D、(y一1)2=8(x一1)(x≠1) |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用抛物线的定义,抛物线上的点到焦点的距离等于到准线的距离,把焦点弦转化为到准线的距离.
解答:
解:设抛物线的焦点为F,抛物线焦点弦的另一个端点Q(x,y);
由P,Q在抛物线上及抛物线的定义:P,Q到焦点的距离等于它们到准线的距离
即|PQ|=|PF|+|QF|=2+1-y=
两端平方化简得:抛物线焦点弦的另一个端点Q的轨迹方程就是(x-1)2=-8(y-1),
故选B
由P,Q在抛物线上及抛物线的定义:P,Q到焦点的距离等于它们到准线的距离
即|PQ|=|PF|+|QF|=2+1-y=
| (x-1)2+(y+1)2 |
两端平方化简得:抛物线焦点弦的另一个端点Q的轨迹方程就是(x-1)2=-8(y-1),
故选B
点评:本题主要考查抛物线的定义,抛物线上的点到焦点的距离等于到准线的距离.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知实数x,y满足不等式组
,则
的取值范围是( )
|
| y+1 |
| x+2 |
| A、(-1,-2] | ||||
B、[
| ||||
C、[
| ||||
D、[
|
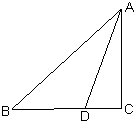 如图,在Rt△ABC(C为直角)中,D为BC边上的一个三等分点(靠近点C),则tan∠BAD的最大值为
如图,在Rt△ABC(C为直角)中,D为BC边上的一个三等分点(靠近点C),则tan∠BAD的最大值为