题目内容
讨论函数f(x)=ax-a-x(a>0且a≠1)的单调性.
考点:函数单调性的性质
专题:函数的性质及应用
分析:f(x1)-f(x2)=ax1-a-x1-ax2+a-x2=(a x1-ax2)(1+
),当a>1时,当0<a<1时分类讨论判断符号即可,得出单调性的结论.
| 1 |
| ax1+x2 |
解答:
解:函数f(x)=ax-a-x(a>0且a≠1)
∵设x1<x2,
∴f(x1)-f(x2)=ax1-a-x1-ax2+a-x2=(a x1-ax2)(1+
),
∵a x1+x2>0,∴1+
>0,
∵,a x1>ax2,
∴(a x1-ax2)(1+
)>0,
即f(x1)>f(x2),
∴当a>1时,函数f(x)=ax-a-x(a>0且a≠1)的单调递增,
∵当0<a<1时,a x1<a x2,
∴(a x1-ax2)(1+
)<0,
即f(x1)<f(x2),
∴当0<a<1时,函数f(x)=ax-a-x(a>0且a≠1)的单调递减.
∵设x1<x2,
∴f(x1)-f(x2)=ax1-a-x1-ax2+a-x2=(a x1-ax2)(1+
| 1 |
| ax1+x2 |
∵a x1+x2>0,∴1+
| 1 |
| ax1+x2 |
∵,a x1>ax2,
∴(a x1-ax2)(1+
| 1 |
| ax1+x2 |
即f(x1)>f(x2),
∴当a>1时,函数f(x)=ax-a-x(a>0且a≠1)的单调递增,
∵当0<a<1时,a x1<a x2,
∴(a x1-ax2)(1+
| 1 |
| ax1+x2 |
即f(x1)<f(x2),
∴当0<a<1时,函数f(x)=ax-a-x(a>0且a≠1)的单调递减.
点评:本题考查了函数的单调性的证明,分类讨论,判断因式的符号问题,关键是分解因式,属于中档题.

练习册系列答案
相关题目
抛物线的准线l的方程是y=l,且抛物线恒过点P(1,一1),则抛物线焦点弦PQ的另一个端点Q的轨迹方程是( )
| A、(x-1)2=-8(y-1) |
| B、(x一1)2=-8(y-1)(x≠1) |
| C、(y一1)2=8(x一1) |
| D、(y一1)2=8(x一1)(x≠1) |
现安排甲、乙等5名同学去参加3个运动项目,要求每个项目都有人参加,每人只参加一个项目,则满足上述要求且甲、乙两人不参加同一个项目的安排方法种数为( )
| A、114 | B、162 |
| C、108 | D、132 |
已知直线l和平面α,无论直线l与平面α具有怎样的位置关系,在平面α内总存在一条直线与直线l( )
| A、相交 | B、平行 | C、垂直 | D、异面 |

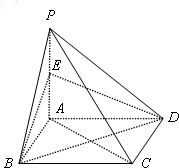 如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点.
如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点. 如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长度为
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长度为