题目内容
已知函数f(x)=log2(1+2x+a4x)的定义域为[1,+∞),求实数a的取值范围 .
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据题意得出t=2x,g(t)=at2+t+1>0,t∈[2,+∞)
运用二次函数求解得出
即可得出;a>0.
运用二次函数求解得出
|
解答:
解:∵函数f(x)=log2(1+2x+a4x)的定义域为[1,+∞),
∴u(x)=1+2x+a(2x)2,x∈[1,+∞),
设t=2x,g(t)=at2+t+1>0,t∈[2,+∞)
∴
解得;a>0.
故答案为:a>0
∴u(x)=1+2x+a(2x)2,x∈[1,+∞),
设t=2x,g(t)=at2+t+1>0,t∈[2,+∞)
∴
|
故答案为:a>0
点评:本题考查了函数的性质,构造法求解范围问题,属于中档题.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积、表面积为( )
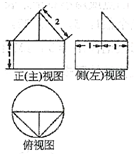

A、π+
| ||||||||
B、2π+
| ||||||||
C、π+
| ||||||||
D、2π+
|
抛物线的准线l的方程是y=l,且抛物线恒过点P(1,一1),则抛物线焦点弦PQ的另一个端点Q的轨迹方程是( )
| A、(x-1)2=-8(y-1) |
| B、(x一1)2=-8(y-1)(x≠1) |
| C、(y一1)2=8(x一1) |
| D、(y一1)2=8(x一1)(x≠1) |

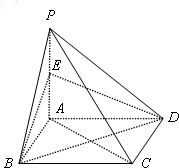 如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点.
如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点. 如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长度为
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过点A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长度为