题目内容
已知圆C的圆心与双曲线
-
=1的右焦点重合,且圆C与双曲线的渐近线相切,则该圆的标准方程是 .
| x2 |
| 16 |
| y2 |
| 9 |
考点:双曲线的简单性质,圆的标准方程
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:根据双曲线的标准方程求出圆心,利用点到直线的距离公式求得半径,从而得到所求的圆的方程.
解答:
解:双曲线
-
=1的右焦点F为(5,0),
一条渐近线为y=
x,即3x-4y=0,
故半径r=
=3,
故所求的圆的方程为(x-5)2+y2=9,
故答案为:(x-5)2+y2=9.
| x2 |
| 16 |
| y2 |
| 9 |
一条渐近线为y=
| 3 |
| 4 |
故半径r=
| |3×5-0| | ||
|
故所求的圆的方程为(x-5)2+y2=9,
故答案为:(x-5)2+y2=9.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,点到直线的距离公式,圆的标准方程,求半径是解题的关键.

练习册系列答案
相关题目
若如图所给程序框图运行的结果恰为s>
,那么判断框中可以填入的关于k的判断条件是( )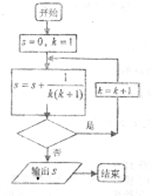
| 2012 |
| 2013 |

| A、k>2013 |
| B、k>2012 |
| C、k<2013 |
| D、k<2012 |
抛物线的准线l的方程是y=l,且抛物线恒过点P(1,一1),则抛物线焦点弦PQ的另一个端点Q的轨迹方程是( )
| A、(x-1)2=-8(y-1) |
| B、(x一1)2=-8(y-1)(x≠1) |
| C、(y一1)2=8(x一1) |
| D、(y一1)2=8(x一1)(x≠1) |
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、若p∨q为真命题,则p,q均为真命题 |
| C、命题“存在x∈R,使得x2+x+1<0”的否定是:“对任意x∈R,均有x2+x+1<0” |
| D、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
现安排甲、乙等5名同学去参加3个运动项目,要求每个项目都有人参加,每人只参加一个项目,则满足上述要求且甲、乙两人不参加同一个项目的安排方法种数为( )
| A、114 | B、162 |
| C、108 | D、132 |
已知定义在R上的函数f(x)的图象是一条连续不断地曲线,且有部分对应值如表所示,那么函数f(x)一定存在零点的区间是( )
| x | 1 | 2 | 3 | ||||
| f(x) | -
| -1 |
|
| A、(-∞,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,+∞) |
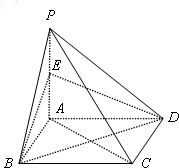 如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点.
如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点.