题目内容
已知|
|=|
|=1，
⊥
，若
=2
+3
，
=m
-4
，
⊥
，则实数m的值为（ ）
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
| A、6 | B、3 | C、-3 | D、-6 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量垂直的性质，将
⊥
利用
，
表示即可．
| c |
| d |
| a |
| b |
解答：
解：∵
=2
+3
，
=m
-4
，
⊥
，
∴
•
=（2
+3
）（m
-4
）=2m
2-12
2+（3m-8）
⊥
=2m-12=0，
∴m=6．
故选A．
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
∴
| c |
| d |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴m=6．
故选A．
点评：本题考查了向量的数量积以及向量垂直的性质；两个向量垂直它们的数量积为0．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若集合A={x|2x-1＜0}，则（ ）
| A、3∈A | B、2∈A |
| C、1∈A | D、-1∈A |
计算结果正确的是（ ）
A、-6x2y3÷
| ||||
B、（-
| ||||
| C、16x5y7÷（-2x3y2）=-32x2y5 | ||||
| D、（2x2y）4÷〔（xy）2]〕2=8x4 |
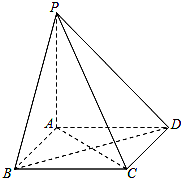如图，在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，且PA=AD．