题目内容
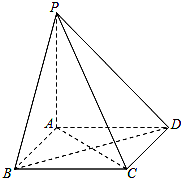 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,且PA=AD.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,且PA=AD.(1)求证:BD⊥平面PAC;
(2)求直线PB与底面ABCD所成的角.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由PA⊥底面ABCD,得PA⊥BD,AC⊥BD,由此能证明BD⊥平面PAC.
(2)由PA⊥底面ABCD,得∠PBA是直线PB与底面ABCD所成的角,由此能求出直线PB与底面ABCD所成的角.
(2)由PA⊥底面ABCD,得∠PBA是直线PB与底面ABCD所成的角,由此能求出直线PB与底面ABCD所成的角.
解答:
(1)证明:∵在四棱锥P-ABCD中,底面ABCD是正方形,
PA⊥底面ABCD,且PA=AD,
∴PA⊥BD,AC⊥BD,
又PA∩AC=A,
∴BD⊥平面PAC.(6分)
(2)∵PA⊥底面ABCD,
∴∠PBA是直线PB与底面ABCD所成的角,
∵PA=AD,
∴∠PBA=45°.
∴直线PB与底面ABCD所成的角为45°.(12分)
PA⊥底面ABCD,且PA=AD,
∴PA⊥BD,AC⊥BD,
又PA∩AC=A,
∴BD⊥平面PAC.(6分)
(2)∵PA⊥底面ABCD,
∴∠PBA是直线PB与底面ABCD所成的角,
∵PA=AD,
∴∠PBA=45°.
∴直线PB与底面ABCD所成的角为45°.(12分)
点评:本题考查直线与平面垂直的证明,考查直线与底面所成的角的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知|
|=|
|=1,
⊥
,若
=2
+3
,
=m
-4
,
⊥
,则实数m的值为( )
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
| A、6 | B、3 | C、-3 | D、-6 |
某商品零售价今年比去年上涨25%,欲控制明年比去年只上涨10%,则明年比今年降价( )
| A、15% | B、10% |
| C、12% | D、50% |
函数y=logx+1(8-2x)的定义域是( )
| A、(-1,3) |
| B、(0,30 |
| C、(-3,1) |
| D、(-1,0)∪(0,3) |
复数1+i+i2+i3+…+i2006=( )
| A、0 | B、1 | C、i | D、1+i |