题目内容

已知集合P={（x，y）|y=2x+b}，Q={（x，y）|y=x2}，如果P∩Q恰有4个不同子集，则实数b的取值范围是
 
．
考点：交集及其运算
专题：集合
分析：根据P∩Q恰有4个不同子集，可知P∩Q恰有2个不同元素，联立直线与曲线方程后化为关于x的一元二次方程，由判别式大于0得答案．
解答： 解：∵集合P={（x，y）|y=2x+b}，Q={（x，y）|y=x2}，
如果P∩Q恰有4个不同子集，则直线y=2x+b与曲线y=x2有两个不同的交点，
联立
y=2x+b
y=x2
，得x2-2x-b=0．
由△=（-2）2+4b＞0，得b＞-1．
∴使P∩Q恰有4个不同子集的实数b的取值范围是（-1，+∞）．
故答案为：（-1，+∞）．
点评：不同考查了交集及其运算，考查了数学转化思想方法，训练了利用判别式法判断方程根的个数，是基础题．
练习册系列答案
相关题目
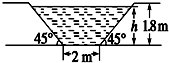如图，某灌溉渠的横断面是等腰梯形，底宽为2m，渠深为1.8m，斜坡的倾斜角是45°．（临界状态不考虑）
（1）试将横断面中水的面积A（m2）表示成水深h（m）的函数；
（2）确定函数的定义域和值域；     
（3）画出函数的图象．
已知函数f（x）=ax2+3x+4，g（x）=ax2+2x-2 （a＞0，a≠1），若f（x）＞g（x），试确定x的范围．
已知集合M={y|y=x2+2x-3，x∈R}，集合N={y||y-2|≤3}，则M∩N=
 
．
化简或求值：
（1）（2
4
5
）0+2-2×(2
1
4
)-
1
2
-(0.01)
1
2
；
（2）2（lg
2
）2+lg
2
•lg5+
(lg
2
)2-lg2+1
．
已知函数f（x）=ax3-2ax+3a-4在区间（-1，1）上有一个零点．
（1）求实数a的取值范围；
（2）若a=
32
17
，用二分法求f（x）=0在区间（-1，1）上的解．（精确到0.1）
5男4女站成一排，分别指出满足下列条件的排法种数
（1）甲站正中间的排法有
 
种，甲不站在正中间的排法有
 
种．
（2）甲、乙相邻的排法有
 
种，甲乙丙三人在一起的排法有
 
种．
（3）甲站在乙前的排法有
 
种，甲站在乙前，乙站在丙前（不要求一定相邻）的排法有
 
种，丙在甲乙之间（不要求一定相邻）的排法有
 
种．
（4）甲乙不站两头的排法有
 
种，甲不站排头，乙不站排尾的排法种有
 
种．
（5）5名男生站在一起，4名女生站在一起的排法有
 
种．
（6）女生互不相邻的排法有
 
种，男女相间的排法有
 
种．
（7）甲与乙、丙都不相邻的排法有
 
种．
（8）甲乙之间有且只有4人的排法有
 
种．
求值：
1-sin2
3π
5
．
已知|
a
|=|
b
|=1，
a
⊥
b
，若
c
=2
a
+3
b
，
d
=m
a
-4
b
，
c
⊥
d
，则实数m的值为（　　）
A、6B、3C、-3D、-6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网