题目内容
若不等式（x-1）2＜logax在x∈（0，1）内恒成立，则实数a的取值范围是 ．
考点：函数恒成立问题
专题：函数的性质及应用
分析：直接作出函数f（x）=（x-1）2，g（x）=logax（0＜a＜1）的图象，由图象即可得到答案．
解答：
解：令f（x）=（x-1）2，g（x）=logax，
作出两个函数的图象如图，
由图可知，满足不等式（x-1）2＜logax在x∈（0，1）内恒成立的实数a的取值范围是（0，1）．
故答案为：（0，1）．
作出两个函数的图象如图，
由图可知，满足不等式（x-1）2＜logax在x∈（0，1）内恒成立的实数a的取值范围是（0，1）．
故答案为：（0，1）．
点评：本题考查了函数恒成立问题，考查了数形结合的解题思想方法，是基础题．
练习册系列答案
相关题目
设Sn是等差数列{an}的前n项和，若a3=7，S12＞0，S13＜0，则下列命题不正确的是（ ）
A、-2＜d＜-
| ||
| B、a1可能为整数 | ||
| C、a6＞0，a7＜0 | ||
| D、在Sn中S6的值最大 |
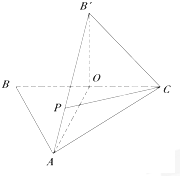如图，△ABC中，O是BC的中点，AB=AC，AO=2OC=2．将△BAO沿AO折起，使B点与图中B'点重合．函数y=-x2+4x-2在区间[0，3]上最大值，最小值分别为（ ）
| A、2和1 | B、2和-1 |
| C、1和-2 | D、2和-2 |