题目内容
16.函数$f(x)=sin(ωx+\frac{π}{6})(ω>0)$与g(x)=sin(2x+θ)对称轴完全相同,将f(x)图象向右平移$\frac{π}{3}$个单位得到h(x),则h(x)的解析式是h(x)=-cos2x.分析 由题意,函数$f(x)=sin(ωx+\frac{π}{6})(ω>0)$与g(x)=sin(2x+θ)对称轴完全相同,可知周期相同,可得ω=2.可得f(x)的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:由题意,函数$f(x)=sin(ωx+\frac{π}{6})(ω>0)$与g(x)=sin(2x+θ)对称轴完全相同,
∴ω=2.
∴f(x)的解析式为:f(x)=sin(2x+$\frac{π}{6}$).
f(x)图象向右平移$\frac{π}{3}$个单位得到sin(2x-$\frac{2π}{3}$+$\frac{π}{6}$)=-cos2x,
∴h(x)=-cos2x,
故答案为:h(x)=-cos2x.
点评 本题主要考查三角函数的性质和函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
7.已知函数f(x)的定义域为R,其图象关于点(1,0)中心对称,其导函数为f′(x),当x<1时,(x-1)[f(x)+(x-1)f′(x)]>0,则不等式xf(x+1)>f(2)的解集为( )
| A. | (-∞,-1) | B. | (1,+∞) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
1.王明参加某卫视的闯关活动,该活动共3关.设他通过第一关的概率为0.8,通过第二、第三关的概率分别为p,q,其中p>q,并且是否通过不同关卡相互独立.记ξ为他通过的关卡数,其分布列为:
(Ⅰ)求王明至少通过1个关卡的概率;
(Ⅱ)求p,q的值.
| ξ | 0 | 1 | 2 | 3 |
| P | 0.048 | a | b | 0.192 |
(Ⅱ)求p,q的值.
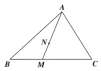 如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.
如图,在△ABC中,M为BC上不同于B,C的任意一点,点N满足$\overrightarrow{AN}=2\overrightarrow{NM}$.若$\overrightarrow{AN}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则x2+9y2的最小值为$\frac{2}{5}$.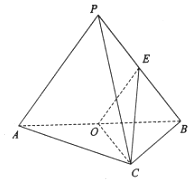 已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.
已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.