题目内容
2．已知函数f（x）=x2-3x，则$\underset{lim}{t→0}$$\frac{f（2）-f（2-3t）}{t}$的值为（ ）| A． | -2 | B． | $\frac{1}{3}$ | C． | 1 | D． | 3 |
分析 先求得f（2）及f（2-3t）的值，代入求极限．
解答 解：则$\underset{lim}{t→0}$$\frac{f（2）-f（2-3t）}{t}$=$\underset{lim}{t→0}$$\frac{-2-（2-3t）^{2}+3（2-3t）}{t}$，
=$\underset{lim}{t→0}$（-9t+3）=3．
故答案选：D．
点评 本题考查极限的值，属于基础题．
练习册系列答案
相关题目
12．执行如图的程序框图，如果输入的t∈[-1，π]，则输出的S属于（ ）
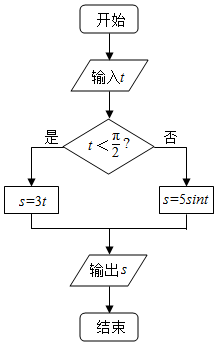
| A． | $[-3，\frac{3π}{2}]$ | B． | $[-5，\frac{3π}{2}]$ | C． | [-5，5] | D． | [-3，5] |
13．点P（1，f（1））是曲线f（x）=x2-2$\sqrt{x}$$+\frac{1}{3}$上的点，设在点P处切线的倾斜角为α，则α的值（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |
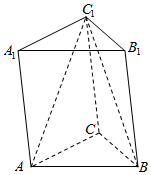如图所示，已知三棱柱ABC-A1B1C1的所有棱长均为1，且AA1⊥底面ABC，则三棱锥C1-ABC的体积为$\frac{\sqrt{3}}{12}$．