题目内容
13.点P(1,f(1))是曲线f(x)=x2-2$\sqrt{x}$$+\frac{1}{3}$上的点,设在点P处切线的倾斜角为α,则α的值( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 求出函数的导数,由导数的几何意义:函数在某点处的导数即为曲线在该点处切线的斜率,代入x=1可得切线的斜率,由直线的斜率公式可得倾斜角.
解答 解:f(x)=x2-2$\sqrt{x}$$+\frac{1}{3}$的导数为f′(x)=2x-$\frac{1}{\sqrt{x}}$,
可得在p(1,f(1))处切线的斜率为2-1=1,
由直线的斜率公式k=tanα(0≤α<π,且α≠$\frac{π}{2}$),
可得倾斜角为$\frac{π}{4}$.
故选:C.
点评 本题考查导数的运用:求切线的斜率和倾斜角,考查导数的几何意义,正确求导是解题的关键,属于基础题.

练习册系列答案
相关题目
2.已知函数f(x)=x2-3x,则$\underset{lim}{t→0}$$\frac{f(2)-f(2-3t)}{t}$的值为( )
| A. | -2 | B. | $\frac{1}{3}$ | C. | 1 | D. | 3 |
3.数列{an}中,an=3n-1,则a2=( )
| A. | 2 | B. | 3 | C. | 9 | D. | 32 |
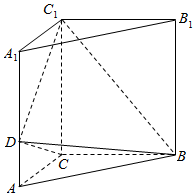 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{2}{5}$AA1,D是棱AA1上的点,且AD=$\frac{1}{4}$DA1.
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=$\frac{2}{5}$AA1,D是棱AA1上的点,且AD=$\frac{1}{4}$DA1.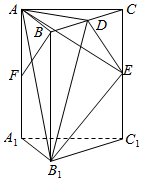 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=1,AC=$\sqrt{3}$,AA1=4,点D、E、F分别是棱BC、CC1、AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=1,AC=$\sqrt{3}$,AA1=4,点D、E、F分别是棱BC、CC1、AA1的中点.


