题目内容
10.已知sin(x+$\frac{π}{6}$)=$\frac{3}{5}$,$\frac{π}{3}$<x<$\frac{5π}{6}$,则cos($\frac{π}{2}$+x)=-$\frac{4+3\sqrt{3}}{10}$.分析 由同角三角函数基本关系可得cos(x+$\frac{π}{6}$),再由诱导公式以及和差角的三角函数公式整体代入计算可得.
解答 解:∵$\frac{π}{3}$<x<$\frac{5π}{6}$,∴$\frac{π}{2}$<x+$\frac{π}{6}$<π,
由sin(x+$\frac{π}{6}$)=$\frac{3}{5}$可得cos(x+$\frac{π}{6}$)=-$\frac{4}{5}$,
∴cos($\frac{π}{2}$+x)=-sinx=-sin[(x+$\frac{π}{6}$)-$\frac{π}{6}$)]
=-$\frac{\sqrt{3}}{2}$sin(x+$\frac{π}{6}$)+$\frac{1}{2}$cos(x+$\frac{π}{6}$)
=-$\frac{\sqrt{3}}{2}$×$\frac{3}{5}$+$\frac{1}{2}$×(-$\frac{4}{5}$)=-$\frac{4+3\sqrt{3}}{10}$,
故答案为:-$\frac{4+3\sqrt{3}}{10}$.
点评 本题考查三角函数化简求值,涉及同角三角函数基本关系以及和差角的三角函数公式,属基础题.

练习册系列答案
相关题目
15.已知a∈R,那么“a>1”是“a2>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
2.已知函数f(x)=x2-3x,则$\underset{lim}{t→0}$$\frac{f(2)-f(2-3t)}{t}$的值为( )
| A. | -2 | B. | $\frac{1}{3}$ | C. | 1 | D. | 3 |
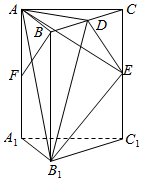 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=1,AC=$\sqrt{3}$,AA1=4,点D、E、F分别是棱BC、CC1、AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=1,AC=$\sqrt{3}$,AA1=4,点D、E、F分别是棱BC、CC1、AA1的中点.



 如图,扇形的半径为r cm,周长为20cm,问扇形的圆心角α等于多少弧度时,这个扇形的面积最大,并求出扇形面积的最大值.
如图,扇形的半径为r cm,周长为20cm,问扇形的圆心角α等于多少弧度时,这个扇形的面积最大,并求出扇形面积的最大值.