题目内容
 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.(Ⅰ)若点G在线段AB上,且BG=3GA,求证:CG∥平面ADF;
(Ⅱ)求直线DE与平面ADF所成的角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)分别取AB,AF的中点M,H,连结MF,GH,DH,由已知条件能推导出四边形CDHG是平行四边形,由此能证明CG∥平面ADF.
(Ⅱ)以B为原点,分别以BC,BE,BA所在直线为x轴,y轴,z轴建立空间直角坐标系O-xyz.利用向量法能求出直线CG与平面ADF所成的角的正弦值.
(Ⅱ)以B为原点,分别以BC,BE,BA所在直线为x轴,y轴,z轴建立空间直角坐标系O-xyz.利用向量法能求出直线CG与平面ADF所成的角的正弦值.
解答:
解:(Ⅰ)分别取AB,AF的中点M,H,连结MF,GH,DH,
则有AG=GM,MF
BE.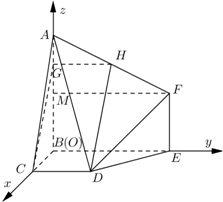
∵AH=HF,
∴GH
MF…(2分)
又∵CD
BE,BE
MF
∴CD
GH
∴四边形CDHG是平行四边形
∴CG∥DH…(4分)
又∵CG?平面ADF,DH?平面ADF
∴CG∥平面ADF…(6分)
(Ⅱ)如图,以B为原点,分别以BC,BE,BA所在直线为x轴,y轴,z轴建立空间直角坐标系O-xyz.
∵AB=BE=2,BC=CD=EF=1,
∴A(0,0,2),C(1,0,0),D(1,1,0),
E(0,2,0),F(0,2,1),
∴
=(-1,1,0),
=(-1,-1,2),
=(0,-2,1)…(7分)
设平面ADF的一个法向量
=(x,y,z),
则有
,化简,得
令y=1,得
=(3,1,2)…(10分)
设直线CG与平面ADF所成的角为θ,
则有sinθ=|
|=
.…(13分)
则有AG=GM,MF
| ||
. |

∵AH=HF,
∴GH
| ||
. |
| 1 |
| 2 |
又∵CD
| ||
. |
| 1 |
| 2 |
| ||
. |
∴CD
| ||
. |
∴四边形CDHG是平行四边形
∴CG∥DH…(4分)
又∵CG?平面ADF,DH?平面ADF
∴CG∥平面ADF…(6分)
(Ⅱ)如图,以B为原点,分别以BC,BE,BA所在直线为x轴,y轴,z轴建立空间直角坐标系O-xyz.
∵AB=BE=2,BC=CD=EF=1,
∴A(0,0,2),C(1,0,0),D(1,1,0),
E(0,2,0),F(0,2,1),
∴
| DE |
| DA |
| FA |
设平面ADF的一个法向量
| n |
则有
|
|
令y=1,得
| n |
设直线CG与平面ADF所成的角为θ,
则有sinθ=|
| ||||
|
|
| ||
| 7 |
点评:本题考查直线与平面平行的证明,考查直线与平面所成角的正弦值的求法,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
 已知ABCD为直角梯形,∠DAB=∠ABC=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.
已知ABCD为直角梯形,∠DAB=∠ABC=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1. 如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点. 如图,在四面体P-ABC中,PA⊥平面ABC,AB⊥BC,PA=2,AC=2
如图,在四面体P-ABC中,PA⊥平面ABC,AB⊥BC,PA=2,AC=2 如图,在正三棱柱ABC-A1B1C1中,AA1=AB=2.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB=2. 如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥AB,AF⊥A1D.
如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥AB,AF⊥A1D.