题目内容
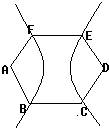 如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为
如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用余弦定理求得AE,由双曲线的定义可得2a=AE-DE 的值,由此求出e的值.
解答:
解:设正六边形ABCDEF的边长为1,中心为O,以AD所在直线为x轴,以O为原点,建立直角坐标系,
则c=1,
在△AEF中,由余弦定理得AE2=AF2+EF2-2AF•EFcos120°=1+1-2(-
)=3,
∴AE=
,2a=AE-DE=
-1,
∴a=
,
∴e=
=
=
+1,
故答案为:
+1.
则c=1,
在△AEF中,由余弦定理得AE2=AF2+EF2-2AF•EFcos120°=1+1-2(-
| 1 |
| 2 |
∴AE=
| 3 |
| 3 |
∴a=
| ||
| 2 |
∴e=
| c |
| a |
| 1 | ||||
|
| 3 |
故答案为:
| 3 |
点评:本题考查双曲线的定义和双曲线的标准方程,以及双曲线的简单性质的应用,计算2a=AE-DE 的值是解题的关键.

练习册系列答案
相关题目
已知AB是⊙O的切线,在下列条件中,能判定AB⊥CD的是( )
| A、AB与⊙O相切于点C,CD为⊙O的一条弦 |
| B、CD过圆心O |
| C、AB与⊙O相切于点C,CD过圆心 |
| D、CD也是⊙O的切线 |
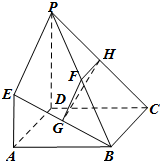 如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.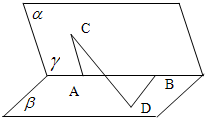 如图,在一个60°的二面角的棱上,有两个点A、B,AC、BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为
如图,在一个60°的二面角的棱上,有两个点A、B,AC、BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4cm,AC=6cm,BD=8cm,则CD的长为