题目内容
过圆x2+y2=1上一点Q作圆的一点切线L,则L和抛物线y=
x2+1有公共点的概率是多少?
| 1 |
| 4 |
考点:直线与圆锥曲线的关系,几何概型,抛物线的标准方程
专题:数形结合,圆锥曲线的定义、性质与方程
分析:设出切线方程,通过切线与抛物线以及圆相切,求出切线的斜率,推出切点之间的圆心角的范围,利用几何概型求出满足题意的概率.
解答:
 解:如图,由题意可知切线的斜率存在.
解:如图,由题意可知切线的斜率存在.
设切线方程为:y=kx+m,m<0.
切线L和抛物线y=
x2+1有公共点,
则
,消去y可得:
x2-kx-m+1=0,∴△=k2+m-1=0…①,
直线L与圆相切,可得
=1…②,
解①②可得,m=1(舍去),或m=-2,此时k=±
,
切线的倾斜角为:
或
,
此时两个切点之间的圆心角为:
,
切线L和抛物线y=
x2+1有公共点的圆心角是
,
切线L和抛物线y=
x2+1有公共点的概率:
=
.
 解:如图,由题意可知切线的斜率存在.
解:如图,由题意可知切线的斜率存在.设切线方程为:y=kx+m,m<0.
切线L和抛物线y=
| 1 |
| 4 |
则
|
| 1 |
| 4 |
直线L与圆相切,可得
| |m| | ||
|
解①②可得,m=1(舍去),或m=-2,此时k=±
| 3 |
切线的倾斜角为:
| π |
| 3 |
| 2π |
| 3 |
此时两个切点之间的圆心角为:
| 2π |
| 3 |
切线L和抛物线y=
| 1 |
| 4 |
| 4π |
| 3 |
切线L和抛物线y=
| 1 |
| 4 |
| ||
| 2π |
| 2 |
| 3 |
点评:本题考查直线与圆锥曲线的位置关系的应用,考查几何概型,直线与圆相切条件的应用,直线的斜率与倾斜角的关系,是综合性比较强题目.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
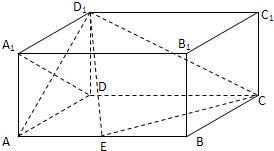 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.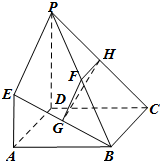 如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.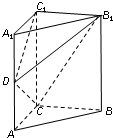 如图,在正三棱柱ABC-A1B1C1中,AA1=AB=2.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB=2.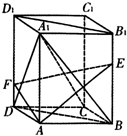 如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥AB,AF⊥A1D.
如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥AB,AF⊥A1D.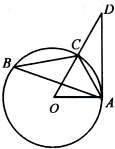 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠OAC=60°,AC=1,则AD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠OAC=60°,AC=1,则AD的长为