题目内容
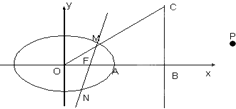 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| a2 |
| c |
| a2 |
| c |
(1)求椭圆C的方程;
(2)求证:N、B、P三点共线;
(3)求△BNM的面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据椭圆
+
=1(a>b>0)经过点T(
,-
),其离心率为
,建立方程组,求出a,b,即可求椭圆C的方程;
(2)分类讨论,证明
,
共线,可得N、B、P三点共线;
(3)分类讨论,表示出△BNM的面积,即可求△BNM的面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
(2)分类讨论,证明
| BP |
| BN |
(3)分类讨论,表示出△BNM的面积,即可求△BNM的面积的最大值.
解答:
(1)解:根据题意得
⇒
,
∴椭圆C的方程为
+
=1;
(2)证明:设直线l:y=k(x-1),M(x1,y1),N(x2,y2),则
直线方程代入椭圆方程,消去y可得(3+4k2)x2-8k2x+4k2-12=0,
∴x1+x2=
,x1x2=
,
∵P(8-x1,y1),
∴
=(4-x1,y1),
=(x2-4,y2),
∴(4-x1)y2)-(x2-4)y1=4k(x1+x2-2)-2kx1x2+k(x1+x2)
=4k(
-2)-2k•
+k•
=0
当l⊥x轴时,也满足,
故
,
共线,
∴N、B、P三点共线;
(3)解:记d为B到l的距离,则d=
,
∴S=
d|MN|=
•
•
•
=
<
当l⊥x轴时,S=
,
∴△BMN的面积的最大值为
.
|
|
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)证明:设直线l:y=k(x-1),M(x1,y1),N(x2,y2),则
直线方程代入椭圆方程,消去y可得(3+4k2)x2-8k2x+4k2-12=0,
∴x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
∵P(8-x1,y1),
∴
| BP |
| BN |
∴(4-x1)y2)-(x2-4)y1=4k(x1+x2-2)-2kx1x2+k(x1+x2)
=4k(
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
| 8k2 |
| 3+4k2 |
当l⊥x轴时,也满足,
故
| BP |
| BN |
∴N、B、P三点共线;
(3)解:记d为B到l的距离,则d=
| 3|k| | ||
|
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3|k| | ||
|
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 9 |
| 2 |
1-
|
| 9 |
| 2 |
当l⊥x轴时,S=
| 9 |
| 2 |
∴△BMN的面积的最大值为
| 9 |
| 2 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
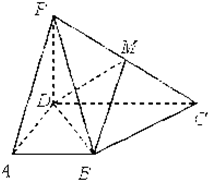 如图,四棱锥P-ABCD中,底面ABCD为梯形,AB∥CD,AD=CD=2AB=2,∠DAB=60°,PD⊥平面ABCD,M为PC的中点
如图,四棱锥P-ABCD中,底面ABCD为梯形,AB∥CD,AD=CD=2AB=2,∠DAB=60°,PD⊥平面ABCD,M为PC的中点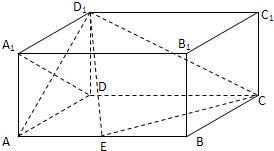 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点.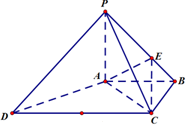 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC= 已知ABCD为直角梯形,∠DAB=∠ABC=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.
已知ABCD为直角梯形,∠DAB=∠ABC=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.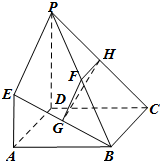 如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.
如图,四边形ABCD是正方形,EA⊥平面ABCD,EA∥PD,AD=PD=2EA,F,G,H分别为PB,EB,PC的中点.