题目内容
春节期间,某单位安排甲、乙、丙三人于正月初一至初五值班,每人至少值班一天,且每人均不能连续值班两天,其中初二不安排甲值班,则共有 种不同的值班安排方案.
考点:排列、组合的实际应用
专题:应用题,排列组合
分析:由题意,由于每人至少值班一天,甲乙丙至少安排1次,则(1)假设剩下的两天是同一个人值的,必然需要ABACA的间隔;(2)剩下的两天是不同人值的,即可得出结论.
解答:
解:由题意,由于每人至少值班一天,甲乙丙至少安排1次,则
(1)假设剩下的两天是同一个人值的,必然需要A甲BACA的间隔,
所以A可以选3种,B可以选2种,C有一种,一共有3×2×1=6种;
(2)剩下的两天是不同人值的,那么有以下的可能
①ABAB,则C可以插在任何位置CABAB,ACBAB,…,ABABC
所以一共3×2×5=30种
②假设是ABBA,那么C只能插在正中间ABCBA
这个一共有3×2×1=6种,
所以加一起有42种,
由于对称性,第二天不安排甲和不安排乙,不安排丙种数是一样的
所以应该是42×
=28种.
(1)假设剩下的两天是同一个人值的,必然需要A甲BACA的间隔,
所以A可以选3种,B可以选2种,C有一种,一共有3×2×1=6种;
(2)剩下的两天是不同人值的,那么有以下的可能
①ABAB,则C可以插在任何位置CABAB,ACBAB,…,ABABC
所以一共3×2×5=30种
②假设是ABBA,那么C只能插在正中间ABCBA
这个一共有3×2×1=6种,
所以加一起有42种,
由于对称性,第二天不安排甲和不安排乙,不安排丙种数是一样的
所以应该是42×
| 2 |
| 3 |
点评:本题考查排列组合知识,考查分类讨论是数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
由0,1,2,3,4这5个数字组成没有重复数字且个位上的数字不能为1的3位数共有( )
| A、28个 | B、36个 |
| C、39个 | D、42个 |
下列命题是真命题的是( )
| A、“若x=2,则(x-2)(x-1)=0” |
| B、“若x=0,则xy=0”的否命题 |
| C、“若x=0,则xy=0”的逆命题 |
| D、“若x>1,则x>2”的逆否命题 |
已知AB是⊙O的切线,在下列条件中,能判定AB⊥CD的是( )
| A、AB与⊙O相切于点C,CD为⊙O的一条弦 |
| B、CD过圆心O |
| C、AB与⊙O相切于点C,CD过圆心 |
| D、CD也是⊙O的切线 |

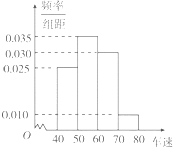 市交警部门计划对翻坝高速联棚至夷陵长江大桥路段进行限速,为调查限速70km/h是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按[40,50),[50,60),[60,70),[70,80)分组,绘制成如图所示的频率分布直方图.则这300辆汽车中车速低于限速的汽车有
市交警部门计划对翻坝高速联棚至夷陵长江大桥路段进行限速,为调查限速70km/h是否合理,对通过该路段的300辆汽车的车速进行检测,将所得数据按[40,50),[50,60),[60,70),[70,80)分组,绘制成如图所示的频率分布直方图.则这300辆汽车中车速低于限速的汽车有