题目内容
13.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F(c,0),作圆x2+y2=$\frac{{a}^{2}}{4}$的切线,切点为E,延长FE交双曲线左支于点M,且E是MF的中点,则双曲线离心率为( )| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | 2$\sqrt{10}$ |
分析 原点O为两焦点的中点,利用中位线的性质,求出PF′的长度及判断出PF′垂直于PF,通过勾股定理得到a,c的关系,进而求出双曲线的离心率.
解答 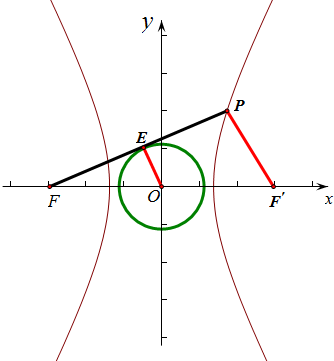 解:如图,记右焦点为F′,则O为FF′的中点,
解:如图,记右焦点为F′,则O为FF′的中点,
∵E为PF的中点,∴OE为△FF′P的中位线,∴PF′=2OE=a,
∵E为切点,∴OE⊥PF,∴PF′⊥PF,
∵点P在双曲线上,∴PF-PF′=2a,∴PF=PF′+2a=3a,
在Rt△PFF′中,有:PF2+PF′2=FF′2,∴9a2+a2=4c2,即10a2=4c2,
∴离心率e=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}=\frac{\sqrt{10}}{2}$,
故选:B.
点评 本题考查双曲线的简单性质、圆的方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.

练习册系列答案
相关题目
8.已知双曲线与 椭圆x2+4y2=64共焦点,它的一条渐近线方程为$x-\sqrt{3}y=0$,则双曲线的方程为$\frac{{x}^{2}}{36}-\frac{{y}^{2}}{12}=1$.
2.函数f(x)=-2x+1(x∈[0,5])的最小、最大值分别为( )
| A. | 3,5 | B. | -9,1 | C. | 1,9 | D. | 1,-9 |
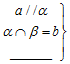 $\end{array}}\right\}$⇒a∥b,在“横线”处补上一个条件使其构成真命题(其中a、b为直线,α,β为平面),这个条件是a∥β.
$\end{array}}\right\}$⇒a∥b,在“横线”处补上一个条件使其构成真命题(其中a、b为直线,α,β为平面),这个条件是a∥β. 已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为x.
已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为x.