题目内容
5. 已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为x.
已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为x.(1)求f($\frac{π}{6}$);
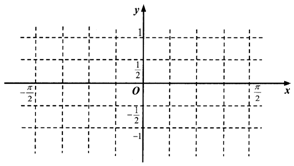
(2)在给定的坐标系中,用列表描点的方法画出函数y=f(x)在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象,并根据图象写出其在[-$\frac{π}{2}$,$\frac{π}{2}$]上的单调递减区间.
分析 (1)依题意先解得ω=2,可得解析式f(x)=sin(2x-$\frac{π}{4}$),从而可求f($\frac{π}{6}$)的值.
(2)先求范围2x-$\frac{π}{4}$∈[-$\frac{5π}{4}$,$\frac{3π}{4}$],列表,描点,连线即可五点法作图象,并根据图象写出其在(-$\frac{π}{2}$,$\frac{π}{2}$)上的单调递减区间.
解答 解:(1)由题意$\frac{2π}{ω}=π$,∴ω=2,
∴f(x)=sin(2x-$\frac{π}{4}$),
∴f($\frac{π}{6}$)=sin($\frac{π}{3}$-$\frac{π}{4}$)=$\frac{\sqrt{6}-\sqrt{2}}{4}$;
(2)∵x∈[-$\frac{π}{2}$,$\frac{π}{2}$],
∴2x-$\frac{π}{4}$∈[-$\frac{5π}{4}$,$\frac{3π}{4}$],
列表如下:
| 2x-$\frac{π}{4}$ | -$\frac{5π}{4}$ | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{3π}{4}$ |
| x | -$\frac{π}{2}$ | -$\frac{3π}{8}$ | -$\frac{π}{8}$ | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{π}{2}$ |
| f(x) | $\frac{\sqrt{2}}{2}$ | 0 | -1 | 0 | 1 | $\frac{\sqrt{2}}{2}$ |

由图象可知函数y=f(x)在(-$\frac{π}{2}$,$\frac{π}{2}$)上的单调递减区间为(-$\frac{π}{2}$,-$\frac{π}{8}$),($\frac{3π}{8}$,$\frac{π}{2}$)
点评 本题主要考察了五点法作函数y=Asin(ωx+φ)的图象,三角函数的图象与性质,属于中档题.

练习册系列答案
相关题目
16.设集合A={x|1<x<2},B={x|x<a}满足A?B,则实数a的取值范围是( )
| A. | [2,+∞) | B. | (-∞,1] | C. | [1,+∞) | D. | (-∞,2] |
13.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F(c,0),作圆x2+y2=$\frac{{a}^{2}}{4}$的切线,切点为E,延长FE交双曲线左支于点M,且E是MF的中点,则双曲线离心率为( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | 2$\sqrt{10}$ |
10.过双曲线x2-$\frac{y^2}{15}$=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x-4)2+y2=4作切线,切点分别为M,N,则|PM|2-|PN|2的最小值为( )
| A. | 10 | B. | 13 | C. | 16 | D. | 19 |
17.从2013年1月1号开始,铁道部对火车票大面积降价,但降价幅度引发了争议.于是,某高校对此展开了一项调查,得到如下数据:
若从参与调查的人员中,按分层抽样的方法抽取50人进行座谈,则给出“差评”与“好评”的人数之差为( )
| 对此事的态度 | 好评(有利于百姓出行) | 中评(影响不大) | 差评(纯属忽悠) | 不关心 |
| 人数 | 2000 | 4000 | 3000 | 1000 |
| A. | 10 | B. | 8 | C. | 5 | D. | 3 |