题目内容
在平面直角坐标系xOy中,已知圆C与x轴交于A(1,0),B(3,0)两点,且与直线x-y-3=0相切,则圆C的半径为 .
考点:圆的切线方程
专题:直线与圆
分析:根据圆C与x轴交于A与B两点,得到AB为圆C的弦,根据垂径定理的逆定理得到圆心C在AB的垂直平分线上,确定出圆心C横坐标为2,设圆心C(2,b),利用两点间的距离公式表示出|AC|的长,即为圆C的半径,由圆C与直线x-y-3=0相切,得到圆心C到直线的距离d=r,利用点到直线的距离公式列出关于b的方程,求出方程的解得到b的值,即可确定出半径.
解答:
解:∵圆C与x轴交于A(1,0),B(3,0)两点,
∴设圆心C坐标为(2,b),半径r=|AC|=
,
∵圆C与直线x-y-3=0相切,
∴圆心C到直线x-y-3=0的距离d=r,即
=
,
解得:b=1,
则圆C的半径r=
=
=
.
故答案为:
∴设圆心C坐标为(2,b),半径r=|AC|=
| b2+1 |
∵圆C与直线x-y-3=0相切,
∴圆心C到直线x-y-3=0的距离d=r,即
| |-1-b| | ||
|
| b2+1 |
解得:b=1,
则圆C的半径r=
| b2+1 |
| 1+1 |
| 2 |
故答案为:
| 2 |
点评:此题考查了圆的切线方程,当直线与圆相切时,圆心到直线的距离等于圆的半径,熟练掌握此性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
对于函数f(x)=cos2(x-
)+sin2(x+
)-1,下列选项中正确的是( )
| π |
| 12 |
| π |
| 12 |
A、f(x)在(
| ||||
| B、f(x)的图象关于原点对称 | ||||
| C、f(x)的最小正周期为2π | ||||
| D、f(x)的最大值为1 |
已知i为虚数单位,若复数
=a+bi(a,b∈R),则a+b=( )
| 1+i |
| 1-i |
| A、-i | B、i | C、-1 | D、1 |
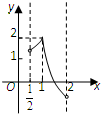


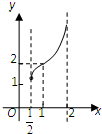
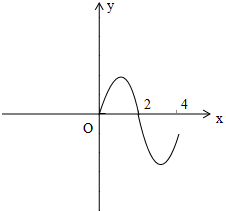 已知奇函数f(x)的定义域为[-4,4],且当x∈[0,4]时,f(x)的函数图象如图所示,解不等式:
已知奇函数f(x)的定义域为[-4,4],且当x∈[0,4]时,f(x)的函数图象如图所示,解不等式: