题目内容
函数f(x)=tan(
x)+log
(x-
)-|tan(
x)-log
(x-
)|在区间(
,2)上的图象大致为( )
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
A、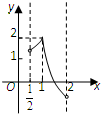 |
B、 |
C、 |
D、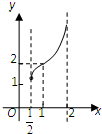 |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:化简f(x)的解析式,去掉绝对值,化f(x)为分段函数,再考查函数在每一段上的增减性即可.
解答:
解:当x∈(
,1)时,f(x)=tan(
x)+log
(x-
)-[log
(x-
)-tan(
x)]
=2tan(
x),函数单调递增;
当x∈[1,2)时,f(x)=tan(
x)+log
(x-
)-[tan(
x)-log
(x-
)]
=2log
(x-
),函数单调递减;
即f(x)=
,
∴满足条件函数f(x)的图象是第一个;
故选:A.
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
=2tan(
| π |
| 4 |
当x∈[1,2)时,f(x)=tan(
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
=2log
| 1 |
| 2 |
| 1 |
| 2 |
即f(x)=
|
∴满足条件函数f(x)的图象是第一个;
故选:A.
点评:本题考查了函数的图象与性质的问题,解题的关键是去掉绝对值,化f(x)为分段函数,考虑函数在每一段上的增减性,是基础题.

练习册系列答案
相关题目
设经过抛物线C的焦点的直线l与抛物线C交于A、B两点,那么抛物线C的准线与以AB为直径的圆的位置关系为( )
| A、相离 | B、相切 |
| C、相交但不经过圆心 | D、相交且经过圆心 |
 如图,在正方体AC1中,E、F分别是AB和AA1的中点,则下列命题:
如图,在正方体AC1中,E、F分别是AB和AA1的中点,则下列命题:①E、C、D1、F四点共面;
②CE、D1F、DA三线共点;
③EF和BD1所成的角为45°;
④A1B∥平面CD1E;
⑤B1D⊥平面CD1E.
其中,正确的个数是( )
| A、2 个 | B、3个 |
| C、4个 | D、5个 |
下列说法正确的是( )
| A、当直线l1与l2的斜率k1,k2满足k1•k2=-1时,两直线一定垂直 | ||||
B、直线Ax+By+C=0的斜率为-
| ||||
C、过(x1,y1),(x2,y2)两点的所有直线的方程
| ||||
| D、经过点(1,1)且在x轴和y轴上截距都相等的直线方程为x+y-2=0 |
已知x,y满足
,且目标函数z=2x+y的最大值是最小值的8倍,则实数a的值是( )
|
| A、1 | ||
B、
| ||
C、
| ||
D、
|
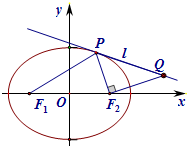 在平面直角坐标系xoy中,已知F1,F2分别是椭圆G:
在平面直角坐标系xoy中,已知F1,F2分别是椭圆G: