题目内容
14.已知a、b、c为△ABC的三边长,若a2=b(b+c),求证:A=2B.分析 延长CA至D,使AD=AB,连接DB.则∠BAC=2∠D.推导出△BCA∽△DCB,由此能证明A=2B.
解答 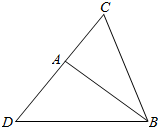 证明:a2=b(b+c),
证明:a2=b(b+c),
即BC2=AC(AC+AB),
延长CA至D,使AD=AB,连接DB.
则∠BAC=2∠D.
∴BC2=AC•CD,$\frac{BC}{AC}=\frac{CD}{BC}$,
又∠C=∠C,
∴△BCA∽△DCB,故∠D=∠ABC.
∴∠BAC=2∠ABC,即A=2B.
点评 本题考查三角形中一个角是另一个角的二倍的证明,是中档题,解题时要认真审题,注意三角形相似的判定定理和性质定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.“a<2”是“实系数一元二次方程x2+ax+1=0有虚根”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知不等式ax2+bx+c<0的解集为(1,2),则不等式$\frac{ax-b}{cx+a}$<0的解集为( )
| A. | (-∞,$\frac{1}{2}$)∪(3,+∞)) | B. | ($\frac{1}{2}$,3) | C. | (-3,-$\frac{1}{2}$) | D. | (-∞,-3)$∪(-\frac{1}{2},+∞)$ |
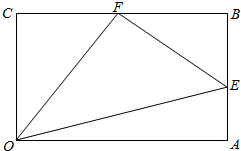 如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.
如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.