题目内容
9.已知:正数m取不同的数值时,方程x2+y2-(4m+2)x-2my+4m2+4m+1=0表示不同的圆,求:这些圆的公切线(即与这些圆都相切的直线)的方程.分析 将圆的方程化为标准方程,表示出圆心坐标与半径,根据题意得到公切线恒过(1,0),设出公切线为y=kx-k,利用点到直线的距离公式列出方程,求出方程的解得到k的值,即可确定出公切线的方程.
解答 解:正数m取不同的数值时,方程x2+y2-(4m+2)x-2my+4m2+4m+1=0,
即[x-(2m+1)]2+(y-m)2=m2,表示以(2m+1,m)为圆心,半径等于|m|的圆,
故圆心所在的直线方程为x-2y-1=0,
当y=0时,x=1,即公切线恒过(1,0),设这些圆的公切线方程为y=kx-k,
圆心到切线的距离d=r,即
| |2mk-mmm| | ||
|
整理得:3k2-4k=0,即k(3k-4)=0,
解得:k=0或k=
| 4 |
| 3 |
则这些圆的公切线方程为y=0或y=
| 4 |
| 3 |
| 4 |
| 3 |
点评 本题主要考查圆系方程,圆的公切线的性质,考查了圆的切线方程,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
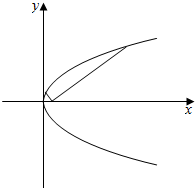 已知顶点在原点,焦点F在x轴上的抛物线过点A(9,6).
已知顶点在原点,焦点F在x轴上的抛物线过点A(9,6).