题目内容
2.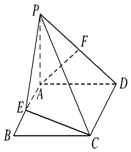 如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.
如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.(1)求证:AF∥平面PCE.
(2)求证:平面PCD⊥平面PCE.
(3)若AD=2,CD=3,求点F到平面PCE的距离.
分析 (1)设M为PC中点,连接ME、MF.推导出四边形AEMF为平行四边形,从而AF∥ME,由此能证明AF∥平面PCE.
(2)推导出△PAD为等腰直角三角形,AF⊥PD,AF⊥CD,从而AF⊥平面PCD.由此能证明平面PCE⊥平面PCD.
(3)过点F作FG⊥PC,交PC于G,FG为点F到平面PCE的距离,由此能求出结果.
解答 证明:(1)设M为PC中点,连接ME、MF.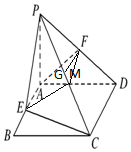
则MF∥$\frac{1}{2}$CD,MF=$\frac{1}{2}$CD,AE∥$\frac{1}{2}$CD,AE=$\frac{1}{2}$CD
∴MF∥AE,MF=AE∴四边形AEMF为平行四边形.…(2分)
∴AF∥ME,又∵ME?平面PCE,AF?平面PCE
∴AF∥平面PCE.…(4分)
(2)∵PA⊥平面ABCD,∠PDA=45°,
∴△PAD为等腰直角三角形,∵PF=FD,
∴AF⊥PD,又∵PA⊥平面ABCD,PA?平面PAD,
∴平面PAD⊥平面ABCD.…(6分)
∵平面PAD∩平面ABCD=AD,
CD⊥AD,CD?平面ABCD.
∴CD⊥平面PAD,∴AF⊥CD,
又∵PD∩CD=D,∴AF⊥平面PCD.
∵EM∥AF,
∴EM⊥平面PCD.
∵EM?平面PCE,
∴平面PCE⊥平面PCD.…(8分)
解:(3)过点F作FG⊥PC,交PC于G,
∵平面PCE⊥平面PCD,∴FG⊥平面PCE,即FG为点F到平面PCE的距离.…(10分)
在Rt△PCD中,PD=2$\sqrt{2}$,PC=$\sqrt{17}$.
∵△PFG∽△PCD,∴$\frac{PF}{PC}$=$\frac{FG}{CD}$,即$\frac{\sqrt{2}}{\sqrt{17}}$=$\frac{FG}{3}$
∴点F到平面PCE的距离FG=$\frac{3\sqrt{34}}{17}$.…(12分)
点评 本题考查线面平行的证明,考查面面垂直的证明,考查点到直线的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | 9 | B. | 9(1-a) | C. | 9-a | D. | 9-a2 |
 某实心钢质工件的三视图如图所示,其中侧视图为等腰三角形,俯视图是一个半径为3的半圆,现将该工件切削加工成一个球体,则该球体的最大体积为( )
某实心钢质工件的三视图如图所示,其中侧视图为等腰三角形,俯视图是一个半径为3的半圆,现将该工件切削加工成一个球体,则该球体的最大体积为( )| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{3π}{2}$ |
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
 运行如图所示的程序框图,当输入实数x的值为-3时,输出的函数值为12,当输入实数x的值为1时,输出的函数值为2.
运行如图所示的程序框图,当输入实数x的值为-3时,输出的函数值为12,当输入实数x的值为1时,输出的函数值为2.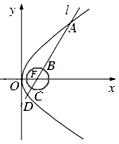 如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆(x-1)2+y2=$\frac{1}{4}$于点A,B,C,D四点,则9|AB|+4|CD|的最小值为$\frac{37}{2}$.
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆(x-1)2+y2=$\frac{1}{4}$于点A,B,C,D四点,则9|AB|+4|CD|的最小值为$\frac{37}{2}$. 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.