题目内容
17．已知a=$\frac{1}{3}$ln$\frac{9}{4}$，b=$\frac{4}{5}$ln$\frac{5}{4}$，c=$\frac{1}{4}$ln4，则下列各式正确的是（ ）| A． | a＜b＜c | B． | b＜a＜c | C． | c＜a＜b | D． | b＜c＜a |
分析 利用对数函数的单调性求解．
解答 解：∵a=$\frac{1}{3}$ln$\frac{9}{4}$=ln$\root{3}{\frac{9}{4}}$，b=$\frac{4}{5}$ln$\frac{5}{4}$=ln$\root{5}{（\frac{5}{4}）^{4}}$，c=$\frac{1}{4}$ln4=ln$\root{4}{4}$=ln$\sqrt{2}$，
y=lnx是增函数，$\root{5}{（\frac{5}{4}）^{4}}$＜$\root{3}{\frac{9}{4}}$＜$\sqrt{2}$，
∴b＜a＜c．
故选：B．
点评 本题考查三个数的大小的比较，是基础题，解题时要认真审题，注意对数函数性质的合理运用．
练习册系列答案
相关题目
8．定义在实数集R上的函数f（x），满足f（x）=f（2-x）=f（x-2），当x∈[0，1]时，f（x）=x•2x．则函数g（x）=f（x）-|lgx|的零点个数为（ ）
| A． | 99 | B． | 100 | C． | 198 | D． | 200 |
5．在空间中，a，b是两条不同的直线，α，β是两个不同的平面，则下列命题中真命题的是（ ）
| A． | 若α∥β，a?α，则a∥β | B． | 若a?α，b?β，α⊥β，则a⊥b | ||
| C． | 若a∥α，a∥b，则b∥α | D． | 若a∥α，b∥α，则a∥b |
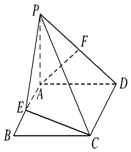如图，PA垂直于矩形ABCD所在的平面，E、F分别是AB、PD的中点，∠ADP=45°．