题目内容
11.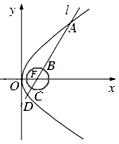 如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆(x-1)2+y2=$\frac{1}{4}$于点A,B,C,D四点,则9|AB|+4|CD|的最小值为$\frac{37}{2}$.
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆(x-1)2+y2=$\frac{1}{4}$于点A,B,C,D四点,则9|AB|+4|CD|的最小值为$\frac{37}{2}$.
分析 求出||AB|=xA+$\frac{1}{2}$,|CD|=xD+$\frac{1}{2}$,当l⊥x轴时,则xD=xA=1,9|AB|+4|CD|=$\frac{39}{2}$.当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,9|AB|+4|CD|=$\frac{13}{2}+9{x}_{A}+4{x}_{D}$$≥\frac{13}{2}+2\sqrt{4×9{x}_{A}{x}_{D}}=\frac{37}{2}$.
解答 解:∵y2=4x,焦点F(1,0),准线 l0:x=-1
由定义得:|AF|=xA+1,
又∵|AF|=|AB|+$\frac{1}{2}$,∴|AB|=xA+$\frac{1}{2}$
同理:|CD|=xD+$\frac{1}{2}$,
当l⊥x轴时,则xD=xA=1,∴9|AB|+4|CD|=$\frac{39}{2}$.
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,xA+xD=1,
∴9|AB|+4|CD|=$\frac{13}{2}+9{x}_{A}+4{x}_{D}$$≥\frac{13}{2}+2\sqrt{4×9{x}_{A}{x}_{D}}=\frac{37}{2}$.
综上所述4|AB|+9|CD|的最小值为$\frac{37}{2}$.
故答案为:$\frac{37}{2}$.
点评 本题考查圆与抛物线的综合,考查基本不等式的运用,考查学生的计算能力,属于中档题

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
1.将函数f(x)=$\sqrt{3}$sinx-cosx的图象向右平移m个单位(m>0),若所得图象对应的函数为偶函数,则m的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{8}$ | D. | $\frac{5π}{6}$ |
19.$\overrightarrow a$=(-1,-5,-2),$\overrightarrow b$=(x,2,x+2),若$\overrightarrow a⊥\overrightarrow b$,则x=( )
| A. | 0 | B. | -6 | C. | $-\frac{14}{3}$ | D. | ±6 |
3.已知直线l1:x+my+7=0和l2:(m-2)x+3y+2m=0互相平行,则实数m=( )
| A. | m=-1或3 | B. | m=-1 | C. | m=-3 | D. | m=1或m=-3 |
20.在${({\sqrt{x}+\frac{3}{x}})^n}$的展开式中,各二项式系数之和为64,则展开式中常数项为( )
| A. | 135 | B. | 105 | C. | 30 | D. | 15 |
1.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若$\overrightarrow{FQ}=-4\overrightarrow{FP}$,则|QF|=( )
| A. | 35 | B. | $\frac{5}{2}$ | C. | 20 | D. | 3 |
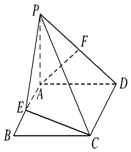 如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.
如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.