题目内容
12．函数f（x）=-ax2+9（a＞0）在[0，3]上的最大值为（ ）| A． | 9 | B． | 9（1-a） | C． | 9-a | D． | 9-a2 |
分析 判断二次函数的对称轴与开口方向，然后求解最值即可．
解答 解：函数f（x）=-ax2+9（a＞0），开口向下，对称轴为：x=0，可知函数的最大值为：f（0）=9．
故选：A．
点评 本题考查二次函数的简单性质的应用，考查计算能力．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
3．函数y=$\frac{lnx}{2x}$的最大值为（ ）
| A． | $\frac{1}{2}$e-1 | B． | e | C． | e2 | D． | $\frac{5}{3}$ |
20．从一批产品中取出三件产品，设A=“三件产品全不是次品”，B=“三件产品全是次品”，C=“三件产品至少有一件是次品”，则下列结论正确的是（ ）
| A． | A与B互斥 | B． | 任何两个均互斥 | C． | B与C互斥 | D． | 任何两个均对立 |
1．将函数f（x）=$\sqrt{3}$sinx-cosx的图象向右平移m个单位（m＞0），若所得图象对应的函数为偶函数，则m的最小值是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{8}$ | D． | $\frac{5π}{6}$ |
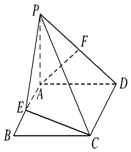如图，PA垂直于矩形ABCD所在的平面，E、F分别是AB、PD的中点，∠ADP=45°．