题目内容
13.东海水晶城大世界营业厅去年利润300万元,今年年初搬迁到新水晶城营业厅,扩大了经营范围.为了获取较大利润,需加大宣传力度.预计从今年起,利润以每年26%的增长率增长,同时在每年12月30日要支付x万元的广告费用.为了实现经过10年利润翻两翻的目标,试求每年用于广告费用x万元的最大值.(注:1.2610≈10.)分析 利用已知条件列出不等式,利用等比数列求和,化简求解即可.
解答 解 由题意得:300×1.2610-1.269x-1.268x-…1.26x-x≥300×4-------(6分)
即300×1.2610-1.269x-1.268x-…1.26x-x≥300×4,$300×{1.26^{10}}-x•\frac{{1-{{1.26}^{10}}}}{1-1.26}≥300×4$,$300×10-x•\frac{9}{0.26}≥300×4$,$300×6≥\frac{9}{0.26}x$,x≤52(万元)--------(14分)
答:每年用于广告费用的最大值为52万元.-------(16分)
点评 本题考查函数的实际应用,等比数列求和,考查计算能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.函数y=$\frac{lnx}{2x}$的最大值为( )
| A. | $\frac{1}{2}$e-1 | B. | e | C. | e2 | D. | $\frac{5}{3}$ |
1.将函数f(x)=$\sqrt{3}$sinx-cosx的图象向右平移m个单位(m>0),若所得图象对应的函数为偶函数,则m的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{8}$ | D. | $\frac{5π}{6}$ |
8.定义在实数集R上的函数f(x),满足f(x)=f(2-x)=f(x-2),当x∈[0,1]时,f(x)=x•2x.则函数g(x)=f(x)-|lgx|的零点个数为( )
| A. | 99 | B. | 100 | C. | 198 | D. | 200 |
18.已知f(x)=x2-bx+a,且f(0)=3,f(2-x)=f(x),则下列关系成立的是( )
| A. | f(bx)≥f(ax) | B. | f(bx)≤f(ax) | ||
| C. | f(bx)<f(ax) | D. | f(bx)与f(ax)的大小关系不确定 |
5.在空间中,a,b是两条不同的直线,α,β是两个不同的平面,则下列命题中真命题的是( )
| A. | 若α∥β,a?α,则a∥β | B. | 若a?α,b?β,α⊥β,则a⊥b | ||
| C. | 若a∥α,a∥b,则b∥α | D. | 若a∥α,b∥α,则a∥b |
3.已知直线l1:x+my+7=0和l2:(m-2)x+3y+2m=0互相平行,则实数m=( )
| A. | m=-1或3 | B. | m=-1 | C. | m=-3 | D. | m=1或m=-3 |
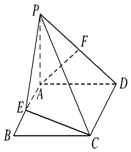 如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.
如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.