题目内容
7. 运行如图所示的程序框图,当输入实数x的值为-3时,输出的函数值为12,当输入实数x的值为1时,输出的函数值为2.
运行如图所示的程序框图,当输入实数x的值为-3时,输出的函数值为12,当输入实数x的值为1时,输出的函数值为2.(1)求函数f(x)的解析式;
(2)当输出结果为80时,求输入的x的值.
分析 (1)根据输入实数x的值为-3时,输出的函数值为12,当输入实数x的值为1时,输出的函数值为2,求得a、b,可得函数f(x)的解析式;
(2)当输出结果为80时,根据分段函数,求输入的x的值.
解答 解:(1)由程序框图知,
∵输入x=-3<0,输出f(-3)=-3b=12,∴b=-4.
∵输入x=1≥0,输出f(1)=a-1=2,∴a=3.
∴f(x)=$\left\{\begin{array}{l}{{3}^{x}-1,x≥0}\\{-4x,x<0}\end{array}\right.$.
(2)由(1)知:
①当x<0时,f(x)=-4x=80,∴x=-20;
②当x≥0时,f(x)=3x-1=80,∴x=4.
综上,输入的x的值为4或-20.
点评 本题借助考查选择结构程序框图,考查了分段函数求函数值,解题的关键是利用程序框图求得分段函数的解析式.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
18.已知f(x)=x2-bx+a,且f(0)=3,f(2-x)=f(x),则下列关系成立的是( )
| A. | f(bx)≥f(ax) | B. | f(bx)≤f(ax) | ||
| C. | f(bx)<f(ax) | D. | f(bx)与f(ax)的大小关系不确定 |
15.已知函数f(x)的定义域是[0,1],则函数F(x)=f[log$\frac{1}{2}$(3-x)]的定义域( )
| A. | {x|0≤x<1} | B. | {x|2≤x<$\frac{5}{2}$} | C. | {x|2≤x≤$\frac{5}{2}$} | D. | {x|2<x≤3} |
19.$\overrightarrow a$=(-1,-5,-2),$\overrightarrow b$=(x,2,x+2),若$\overrightarrow a⊥\overrightarrow b$,则x=( )
| A. | 0 | B. | -6 | C. | $-\frac{14}{3}$ | D. | ±6 |
17.已知实数x,y满足x2+4y2≤4,则|x+2y-4|+|3-x-y|的最大值为( )
| A. | 6 | B. | 12 | C. | 13 | D. | 14 |
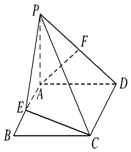 如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.
如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.