题目内容
14.已知集合A={x|$\frac{3}{x}$<1},集合B={y|y=t-2$\sqrt{t-3}$},则A∩B={x|x>3}.分析 分别求出关于A、B的范围,求出A、B的交集即可.
解答 解:A={x|$\frac{3}{x}$<1}={x|x>3或x<0},
B={y|y=t-2$\sqrt{t-3}$}={y|y=${(\sqrt{t-3}-1)}^{2}$+2}={y|y≥2},
则A∩B={x|x>3},
故答案为:{x|x>3}.
点评 本题考查了不等式的解法以及二次函数的性质,考查集合的交集的运算,是一道基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
5.在空间中,a,b是两条不同的直线,α,β是两个不同的平面,则下列命题中真命题的是( )
| A. | 若α∥β,a?α,则a∥β | B. | 若a?α,b?β,α⊥β,则a⊥b | ||
| C. | 若a∥α,a∥b,则b∥α | D. | 若a∥α,b∥α,则a∥b |
19.$\overrightarrow a$=(-1,-5,-2),$\overrightarrow b$=(x,2,x+2),若$\overrightarrow a⊥\overrightarrow b$,则x=( )
| A. | 0 | B. | -6 | C. | $-\frac{14}{3}$ | D. | ±6 |
3.已知直线l1:x+my+7=0和l2:(m-2)x+3y+2m=0互相平行,则实数m=( )
| A. | m=-1或3 | B. | m=-1 | C. | m=-3 | D. | m=1或m=-3 |
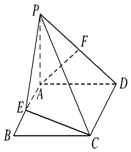 如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.
如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.