题目内容
10. 某实心钢质工件的三视图如图所示,其中侧视图为等腰三角形,俯视图是一个半径为3的半圆,现将该工件切削加工成一个球体,则该球体的最大体积为( )
某实心钢质工件的三视图如图所示,其中侧视图为等腰三角形,俯视图是一个半径为3的半圆,现将该工件切削加工成一个球体,则该球体的最大体积为( )| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{3π}{2}$ |
分析 由三视图知几何体为半个圆锥,根据三视图的数据求底面面积与高,求出其轴截面的内切球的半径,代入公式计算即可.
解答 解:由题目所给三视图可得,该几何体为圆锥的一半,圆锥的底面半径为3,高为4,所以母线长为5,
设其轴截面的内切球的半径为r,则$\frac{1}{2}×(3+4+5)r=\frac{1}{2}×3×4$,∴r=1,
∴该球体的最大体积为$\frac{4}{3}π$,
故选A.
点评 本题考查三视图求表面积、体积,考查空间想象能力,计算能力,是基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
20.从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品至少有一件是次品”,则下列结论正确的是( )
| A. | A与B互斥 | B. | 任何两个均互斥 | C. | B与C互斥 | D. | 任何两个均对立 |
1.将函数f(x)=$\sqrt{3}$sinx-cosx的图象向右平移m个单位(m>0),若所得图象对应的函数为偶函数,则m的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{8}$ | D. | $\frac{5π}{6}$ |
18.已知f(x)=x2-bx+a,且f(0)=3,f(2-x)=f(x),则下列关系成立的是( )
| A. | f(bx)≥f(ax) | B. | f(bx)≤f(ax) | ||
| C. | f(bx)<f(ax) | D. | f(bx)与f(ax)的大小关系不确定 |
5.在空间中,a,b是两条不同的直线,α,β是两个不同的平面,则下列命题中真命题的是( )
| A. | 若α∥β,a?α,则a∥β | B. | 若a?α,b?β,α⊥β,则a⊥b | ||
| C. | 若a∥α,a∥b,则b∥α | D. | 若a∥α,b∥α,则a∥b |
15.已知函数f(x)的定义域是[0,1],则函数F(x)=f[log$\frac{1}{2}$(3-x)]的定义域( )
| A. | {x|0≤x<1} | B. | {x|2≤x<$\frac{5}{2}$} | C. | {x|2≤x≤$\frac{5}{2}$} | D. | {x|2<x≤3} |
19.$\overrightarrow a$=(-1,-5,-2),$\overrightarrow b$=(x,2,x+2),若$\overrightarrow a⊥\overrightarrow b$,则x=( )
| A. | 0 | B. | -6 | C. | $-\frac{14}{3}$ | D. | ±6 |
20.在${({\sqrt{x}+\frac{3}{x}})^n}$的展开式中,各二项式系数之和为64,则展开式中常数项为( )
| A. | 135 | B. | 105 | C. | 30 | D. | 15 |
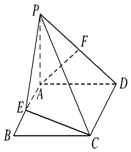 如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.
如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.