题目内容
9.某人欲把a,b两盆红色花和c,d两盆紫色花放在一排四个花台上,若b,c两盆花必须相邻,则不同的放法共有12种.分析 b,c两盆花必须相邻,利用捆绑法与其余2盆红色花全排即可.
解答 解:由题意,利用捆绑法,b,c两盆花必须相邻的方法数为A33•A22=12种.
故答案为:12.
点评 本题主要考查排列与组合及两个基本原理,正确运用捆绑法是关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
20.设等差数列{an}满足a2=7,a4=3,Sn是数列{an}的前n项和,则使得Sn>0最大的自然数n是( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
14.已知命题p:?x≥0,2x≥1;命题q:若x>y,则x2>y2.则下列命题为真命题的是( )
| A. | p∧q | B. | p∧¬q | C. | ¬p∧¬q | D. | ¬p∨q |
18.设Sn为等差数列{an}的前n项和,且a1+a10-a5=6,则S11=( )
| A. | 55 | B. | 66 | C. | 110 | D. | 132 |
19.命题“?x∈R,x2+2x+2>0”的否定是( )
| A. | ?x∈R,x2+2x+2≤0 | B. | ?x∈R,x2+2x+2≤0 | C. | ?x∈R,x2+2x+2<0 | D. | ?x∈R,x2+2x+2>0 |
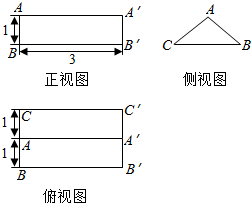 如图是一个几何体的三视图(单位:cm).
如图是一个几何体的三视图(单位:cm).