题目内容
19.命题“?x∈R,x2+2x+2>0”的否定是( )| A. | ?x∈R,x2+2x+2≤0 | B. | ?x∈R,x2+2x+2≤0 | C. | ?x∈R,x2+2x+2<0 | D. | ?x∈R,x2+2x+2>0 |
分析 根据全称命题的否定要改成存在性命题的原则,可写出原命题的否定.
解答 解:原命题为:?x∈R,x2+2x+2>0,
∵原命题为全称命题,
∴其否定为存在性命题,且不等号须改变,
∴原命题的否定为:?x∈R,x2+2x+2≤0.
故选:B.
点评 本题考查命题的否定的写法,常见的命题的三种形式写否定:(1)“若A,则B”的否定为“若¬A,则¬B”;(2)全称命题的否定为存在性命题,存在性命题的否定为全称命题;(3)切命题的否定为或命题,或命题的否定为切命题.本题考查第二种形式,属简单题.

练习册系列答案
相关题目
7.设抛物线C:y2=8x的焦点为F,过F的直线与C相交于A,B两点,记点F到直线l:x=-2的距离为d,则有( )
| A. | |AB|=2d | B. | |AB|≥2d | C. | |AB|≤2d | D. | |AB|<2d |
14.(x2-2)(1+$\frac{2}{x}$)5的展开式中x-1的系数为( )
| A. | 60 | B. | 50 | C. | 40 | D. | 20 |
11.已知正方体ABCD-A′B′C′D′,点E是A′C′的中点,点F是AE的三等分点,且$AF=\frac{1}{2}EF$,则$\overrightarrow{AF}$等于( )
| A. | $\overrightarrow{AA′}$+$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | B. | $\frac{1}{2}$$\overrightarrow{AA′}$+$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | C. | $\frac{1}{2}$$\overrightarrow{AA′}$+$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AD}$ | D. | $\frac{1}{3}$$\overrightarrow{AA′}$+$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AD}$ |
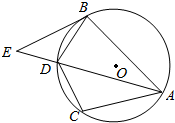 如图,A,B,C,D是半径为1的⊙O上的点,BD=DC=1,⊙O在点B处的切线交AD的延长线于点E.
如图,A,B,C,D是半径为1的⊙O上的点,BD=DC=1,⊙O在点B处的切线交AD的延长线于点E.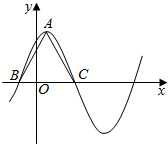 函数$f(x)=6{cos^2}\frac{ωx}{2}+\sqrt{3}sinωx-3({ω>0})$在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
函数$f(x)=6{cos^2}\frac{ωx}{2}+\sqrt{3}sinωx-3({ω>0})$在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.