题目内容
已知f(n)=1+2+3+…+(n-1)+n+(n-1)+…+3+2+1,对任意n∈N*,f(n+1)-f(n)= .
考点:数列的求和,数列的函数特性
专题:点列、递归数列与数学归纳法
分析:利用倒序相加法求出f(n),进一步求得f(n+1),与f(n)作差后得答案.
解答:
解:∵f(n)=1+2+3+…+(n-1)+n+(n-1)+…+3+2+1
=2[1+2+3+…+(n-1)]+n
=2×
+n=n2.
∴f(n+1)-f(n)=(n+1)2-n2=2n+1.
故答案为:2n+1.
=2[1+2+3+…+(n-1)]+n
=2×
| (1+n-1)(n-1) |
| 2 |
∴f(n+1)-f(n)=(n+1)2-n2=2n+1.
故答案为:2n+1.
点评:本题考查倒序相加法求数列的和,考查了学生观察问题和分析问题的能力,是中低档题.

练习册系列答案
相关题目
 如图过抛物线y2=4x焦点F的直线与抛物线交于A,B两点,直线AO交抛物线准线于C点.
如图过抛物线y2=4x焦点F的直线与抛物线交于A,B两点,直线AO交抛物线准线于C点.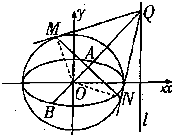 如图,已知椭圆
如图,已知椭圆 如图,为了测量点A与河流对岸点B之间的距离,在点A同侧选取点C,若测得AC=40米,∠BAC=75°,∠ACB=60°,则点A与点B之间的距离等于
如图,为了测量点A与河流对岸点B之间的距离,在点A同侧选取点C,若测得AC=40米,∠BAC=75°,∠ACB=60°,则点A与点B之间的距离等于