题目内容
已知f（x）是定义在实数集R上的增函数，且f（1）=0，函数g（x）在（-∞，1]上为增函数，在[1，+∞）上为减函数，且g（2）=g（0）=0，则集合{x|
≥0}等于（ ）
| f(x) |
| g(x) |
| A、{x|x＜0或1≤x＜2} |
| B、{x|0＜x＜2} |
| C、{x|x≤2} |
| D、{x|0＜x≤1或x＞2} |
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：根据函数奇偶性和单调性之间的关系，即可得到结论．
解答：
解：由题意，结合函数性质可得x＞1，f（x）＞0，x＜1，f（x）＜0，x＜0或x＞2时g（x）＜0，0＜x＜2时g（x）＞0，
故
≥0的解集为{x|x＜0或1≤x＜2}．
故选：A．
故
| f(x) |
| g(x) |
故选：A．
点评：本题主要考查不等式的求解，根据函数奇偶性和单调性之间的关系是解决本题的关键．
练习册系列答案
相关题目
在△ABC中，内角A，B，C所对的边分别是a，b，c，已知b-c=
a，2sinB=3sinC，则cos（B+C）=（ ）
| 1 |
| 4 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
定积分
（ex+x）dx的值为（ ）
| ∫ | 2 0 |
| A、e2-1 |
| B、e2 |
| C、e2+1 |
| D、e2+2 |
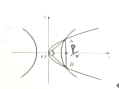如图，双曲线