题目内容
已知实数a,b满足1003a+1004b=2006b,997a+1009b=2007a,则a与b的大小关系为( )
| A、a<b | B、a>b |
| C、a≤b | D、a≥b |
考点:不等式比较大小
专题:函数的性质及应用
分析:由题意,根据任何正数的实数次幂都为正数,得出1003a>0,1004b>0,2006b>0,再由两式得出b、a都是大于0的,不妨令b=1,即可得出a、b的大小.
解答:
解:∵1003a+1004b=2006b①,997a+1009b=2007a②,
且任何正数的实数次幂都为正数;
∴对①式:1003a>0,1004b>0,2006b>0,
由1003a+1004b=2006b得,1004b<2006b,∴b>0;
对②式,同理得a>0;
由①式,不妨令b=1,则1003a=1002,∴a<1,即a<b;
综上,a与b的大小关系为a<b.
故选:A.
且任何正数的实数次幂都为正数;
∴对①式:1003a>0,1004b>0,2006b>0,
由1003a+1004b=2006b得,1004b<2006b,∴b>0;
对②式,同理得a>0;
由①式,不妨令b=1,则1003a=1002,∴a<1,即a<b;
综上,a与b的大小关系为a<b.
故选:A.
点评:本题考查了比较大小的问题,解题时应灵活应用特殊值方法,是易错题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
为了得到函数y=3cos(2x-
)的图象,只需要把函数y=3cos(2x)的图象上所有的点( )
| π |
| 3 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
设l,m是两条不同的直线,a是一个平面,则下列命题正确的是( )
| A、若l⊥m,m⊥a,则l∥a |
| B、若m⊥l,l?a,则m⊥a |
| C、若m∥l,l∥a,则m∥a |
| D、若l⊥a,m⊥a,则l∥m |
 已知椭圆C:
已知椭圆C: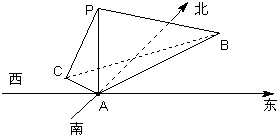 在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午9时测得一轮船在海岛北偏东30°,俯角为30°的B处,匀速直行10分钟后,测得该船位于海岛北偏西60°,俯角为45°的C处.从C处开始,该船航向改为正南方向,且速度大小不变,则该船经过10分钟后离开A点的距离为( )
在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午9时测得一轮船在海岛北偏东30°,俯角为30°的B处,匀速直行10分钟后,测得该船位于海岛北偏西60°,俯角为45°的C处.从C处开始,该船航向改为正南方向,且速度大小不变,则该船经过10分钟后离开A点的距离为( )