Question

已知椭圆C的中点在原点，焦点在x轴上，离心率等于

1

2

，它的一个顶点恰好是抛物线x²=8

3

y的焦点．
（1）求椭圆C的方程；
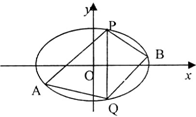
（2）已知点P（2，3），Q（2，-3）在椭圆上，点A、B是椭圆上不同的两个动点，且满足∠APQ=∠BPQ，试问直线AB的斜率是否为定值，请说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由已知条件设椭圆C的方程为

x2

a2

+

y2

b2

=1，并且b=2

3

，

c

a

=

1

2

，由此能求出椭圆C的方程．
（2）由已知条件设PA的直线方程为y-3=k（x-2），PB的直线方程为y-3=-k（x-2），A（x₁，y₁），B（x₂，y₂），由已知条件推导出x1+x2=

16k2-12

3+4k2

，x1-x2=

-48k

3+4k2

，由此能求出AB的斜率为定值．

解答： 解：（1）∵椭圆C的中点在原点，焦点在x轴上，
∴设椭圆C的方程为

x2

a2

+

y2

b2

=1，a＞b＞0，
离心率等于

1

2

，它的一个顶点恰好是抛物线x²=8

3

y的焦点，
∴b=2

3

，

c

a

=

1

2

，
∵a²=b²+c²，∴a=4，
∴椭圆C的方程为

x2

16

+

y2

12

=1．
（2）当∠APQ=∠BPQ时，PA，PB的斜率之和为0，
设直线PA的斜为k，则PB的斜率为-k，设A（x₁，y₁），B（x₂，y₂），
设PA的直线方程为y-3=k（x-2），
由

y-3=k(x-2) x2 16 + y2 12 =1

，消去y并整理，得：
（3+4k²）x²+8（3-2k）kx+4（3-2k²）-48=0，
∴x1+2=

8(2k-3)k

3+4k2

，
设PB的直线方程为y-3=-k（x-2），
同理，得x2+2=

-8k(-2k-3)

3+4k2

=

8k(2k+3)

3+4k2

，
∴x1+x2=

16k2-12

3+4k2

，x1-x2=

-48k

3+4k2

，
k_AB=

y1-y2

x1-x2

=

k(x1-2)+3+k(x2-2)-3

x1-x2

=

k(x1+x2)-4k

x1-x2

=

1

2

，
∴AB的斜率为定值

1

2

．

点评：本题考查椭圆方程的求法，考查直线的斜率为定值的证明，解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化．