题目内容
函数f（x）=2x2-mx+5，当x∈[-1，+∞）时是增函数，当x∈（-∞，-1]时是减函数，则f（-2）等于（ ）
| A、5 | B、7 |
| C、9 | D、由m的值而定的常数 |
考点：二次函数的性质
专题：函数的性质及应用
分析：由已知中函数的单调性，可得x=-1为二次函数图象的对称轴，进而求出m值后，可得函数解析式，进而得到答案．
解答：
解：∵当x∈[-1，+∞）时是增函数，当x∈（-∞，-1]时是减函数，
∴x=-1为二次函数图象的对称轴，
∴
=-1，即m=-4，
∴f（x）=2x2+4x+5，
f（-2）=8-8+5=5．
故选：A
∴x=-1为二次函数图象的对称轴，
∴
| m |
| 4 |
∴f（x）=2x2+4x+5，
f（-2）=8-8+5=5．
故选：A
点评：本题考查的知识点是二次函数的性质，其中求出函数的解析式是解答的关键．
练习册系列答案
相关题目
下列命题：
（1）函数y=
+x(x＜0)的值域是（-∞，-2]；
（2）函数y=x2+2+
最小值是2；
（3）若a，b同号且a≠b，则
+
＞2．
其中正确的命题是（ ）
（1）函数y=
| 1 |
| x |
（2）函数y=x2+2+
| 1 |
| x2+2 |
（3）若a，b同号且a≠b，则
| a |
| b |
| b |
| a |
其中正确的命题是（ ）
| A、（1）（2）（3） |
| B、（1）（2） |
| C、（2）（3） |
| D、（1）（3） |
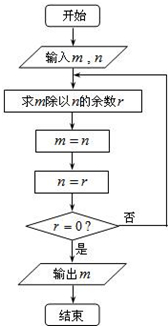如图所示的程序框图描述的算法称为欧几里得辗转相除法，若输入m=2010，n=1541，则输出的m的值为（ ）| A、2010 | B、1541 |
| C、134 | D、67 |
记等比数列{an}的前n项积为Πn，若a4•a5=2，则Π8=（ ）
| A、256 | B、81 | C、16 | D、1 |
一算法的程序框图如右图所示，若输出的y=
，则输入的x可能为（ ）
| 1 |
| 2 |
| A、-1 | B、0 | C、1 | D、5 |
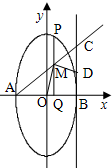已知椭圆：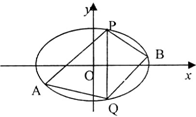
已知椭圆C的中点在原点，焦点在x轴上，离心率等于