题目内容
已知函数f(x)=x3-x-
.
(I)求函数y=f(x)的零点的个数;
(Ⅱ)令g(x)=
+lnx,若函数y=g(x)在(0,
)内有极值,求实数a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,对任意t∈(1,+∞),s∈(0,1),求证:g(t)-g(s)>e+2-
.
| x |
(I)求函数y=f(x)的零点的个数;
(Ⅱ)令g(x)=
| ax2+ax | ||
f(x)+
|
| 1 |
| e |
(Ⅲ)在(Ⅱ)的条件下,对任意t∈(1,+∞),s∈(0,1),求证:g(t)-g(s)>e+2-
| 1 |
| e |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)易知x=0是y=f(x)的零点,从而x>0时,f(x)=x(x2-1-
),设φ(x)=x2-1-
,利用导数及零点判定定理可求函数零点个数;
(Ⅱ)化简得g(x)=lnx+
,其定义域是(0,1)∪(1,+∞),求导得g'(x)=
,令h(x)=x2-(2+a)x+1,则问题转化为h(x)=0有两个不同的根x1,x2,从而△=(2+a)2-4>0,且一根在(0,
)内,不妨设0<x1<
,再由x1x2=1,得0<x1<
<e<x2,根据零点判定定理可知只需h(
)<0,由此可求a的范围;
(Ⅲ)由(Ⅱ)可求y=g(x)在(1,+∞)内的最小值为g(x2),y=g(x)在(0,1)内的最大值为g(x1),由(Ⅱ)同时可知x1+x2=2+a,x1x2=1,x1∈(0,
),x2∈(e,+∞),故g(t)-g(s)≥g(x2)-g(x1)=lnx2+
-lnx1-
=ln
+
-
=lnx22+x2-
(x2>e),令k(x)=lnx2+x-
=2lnx+x-
,利用导数可判断k(x)在(e,+∞)内单调递增,从而有k(x)>k(e),整理可得结论;
| 1 | ||
|
| 1 | ||
|
(Ⅱ)化简得g(x)=lnx+
| a |
| x-1 |
| x2-(2+a)x+1 |
| x(x-1)2 |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
(Ⅲ)由(Ⅱ)可求y=g(x)在(1,+∞)内的最小值为g(x2),y=g(x)在(0,1)内的最大值为g(x1),由(Ⅱ)同时可知x1+x2=2+a,x1x2=1,x1∈(0,
| 1 |
| e |
| a |
| x2-1 |
| a |
| x1-1 |
| x2 |
| x1 |
| a |
| x2-1 |
| a |
| x1-1 |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
解答:
解:(Ⅰ)∵f(0)=0,∴x=0是y=f(x)的一个零点,
当x>0时,f(x)=x(x2-1-
),设φ(x)=x2-1-
,
φ'(x)=2x+
>0,∴φ(x)在(0,+∞)上单调递增.
又φ(1)=-1<0,φ(2)=3-
>0,
故φ(x)在(1,2)内有唯一零点,
因此y=f(x)在(0,+∞)内有且仅有2个零点;
(Ⅱ)g(x)=
+lnx=
+lnx=lnx+
,
其定义域是(0,1)∪(1,+∞),
则g'(x)=
-
=
=
,
设h(x)=x2-(2+a)x+1,要使函数y=g(x)在(0,
)内有极值,则h(x)=0有两个不同的根x1,x2,
∴△=(2+a)2-4>0,得a>0或a<-4,且一根在(0,
)内,不妨设0<x1<
,
又x1x2=1,∴0<x1<
<e<x2,
由于h(0)=1,则只需h(
)<0,即
-(a+2)•
+1<0,
解得a>e+
-2;
(Ⅲ)由(Ⅱ)可知,当x∈(1,x2)时,g'(x)<0,g(x)递减,x∈(x2,+∞)时,g'(x)>0,g(x)递增,
故y=g(x)在(1,+∞)内的最小值为g(x2),即t∈(1,+∞)时,g(t)≥g(x2),
又当x∈(0,x1)时,g'(x)>0,g(x)单调递增,x∈(x1,1)时,g'(x)<0,g(x)单调递减,
故y=g(x)在(0,1)内的最大值为g(x1),即对任意s∈(0,1),g(s)≤g(x1),
由(Ⅱ)可知x1+x2=2+a,x1x2=1,x1∈(0,
),x2∈(e,+∞),
因此,g(t)-g(s)≥g(x2)-g(x1)=lnx2+
-lnx1-
=ln
+
-
=lnx22+x2-
(x2>e),
设k(x)=lnx2+x-
=2lnx+x-
,k'(x)=
+1+
>0,
∴k(x)在(e,+∞)内单调递增,
故k(x)>k(e)=2+e-
,即g(t)-g(s)>e+2-
.
当x>0时,f(x)=x(x2-1-
| 1 | ||
|
| 1 | ||
|
φ'(x)=2x+
| 1 | ||
2
|
又φ(1)=-1<0,φ(2)=3-
| 1 | ||
|
故φ(x)在(1,2)内有唯一零点,
因此y=f(x)在(0,+∞)内有且仅有2个零点;
(Ⅱ)g(x)=
| ax2+ax |
| x3-x |
| ax(x+1) |
| x(x+1)(x-1) |
| a |
| x-1 |
其定义域是(0,1)∪(1,+∞),
则g'(x)=
| 1 |
| x |
| a |
| (x-1)2 |
| x2-2x+1-ax |
| x(x-1)2 |
| x2-(2+a)x+1 |
| x(x-1)2 |
设h(x)=x2-(2+a)x+1,要使函数y=g(x)在(0,
| 1 |
| e |
∴△=(2+a)2-4>0,得a>0或a<-4,且一根在(0,
| 1 |
| e |
| 1 |
| e |
又x1x2=1,∴0<x1<
| 1 |
| e |
由于h(0)=1,则只需h(
| 1 |
| e |
| 1 |
| e2 |
| 1 |
| e |
解得a>e+
| 1 |
| e |
(Ⅲ)由(Ⅱ)可知,当x∈(1,x2)时,g'(x)<0,g(x)递减,x∈(x2,+∞)时,g'(x)>0,g(x)递增,
故y=g(x)在(1,+∞)内的最小值为g(x2),即t∈(1,+∞)时,g(t)≥g(x2),
又当x∈(0,x1)时,g'(x)>0,g(x)单调递增,x∈(x1,1)时,g'(x)<0,g(x)单调递减,
故y=g(x)在(0,1)内的最大值为g(x1),即对任意s∈(0,1),g(s)≤g(x1),
由(Ⅱ)可知x1+x2=2+a,x1x2=1,x1∈(0,
| 1 |
| e |
因此,g(t)-g(s)≥g(x2)-g(x1)=lnx2+
| a |
| x2-1 |
| a |
| x1-1 |
| x2 |
| x1 |
| a |
| x2-1 |
| a |
| x1-1 |
| 1 |
| x2 |
设k(x)=lnx2+x-
| 1 |
| x |
| 1 |
| x |
| 2 |
| x |
| 1 |
| x2 |
∴k(x)在(e,+∞)内单调递增,
故k(x)>k(e)=2+e-
| 1 |
| e |
| 1 |
| e |
点评:本题考查利用导数研究函数的零点、极值、最值,考查转化思想,考查学生综合运用数学知识分析解决问题的能力,综合性强,能力要求比较高.

练习册系列答案
相关题目
记等比数列{an}的前n项积为Πn,若a4•a5=2,则Π8=( )
| A、256 | B、81 | C、16 | D、1 |
如图所示程序框图中,输出S=( )
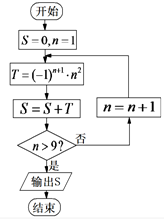

| A、45 | B、-55 |
| C、-66 | D、66 |
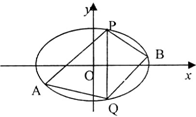 已知椭圆C的中点在原点,焦点在x轴上,离心率等于
已知椭圆C的中点在原点,焦点在x轴上,离心率等于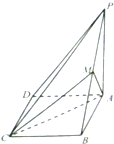 如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=
如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC= 已知直线l:y=2x与抛物线C:y=
已知直线l:y=2x与抛物线C:y=