题目内容
方程
+
=1表示的曲线为C,则给出的下面四个命题:
(1)曲线C不能是圆
(2)若1<k<4,则曲线C为椭圆
(3)若曲线C为双曲线,则k<1或k>4
(4)若曲线C表示焦点在x轴上的椭圆,则1<k<
其中正确的命题是 (填序号)
| x2 |
| 4-k |
| y2 |
| k-1 |
(1)曲线C不能是圆
(2)若1<k<4,则曲线C为椭圆
(3)若曲线C为双曲线,则k<1或k>4
(4)若曲线C表示焦点在x轴上的椭圆,则1<k<
| 5 |
| 2 |
其中正确的命题是
考点:命题的真假判断与应用
专题:圆锥曲线的定义、性质与方程,简易逻辑
分析:根据曲线方程的特点,结合圆、椭圆、双曲线的标准方程分别判断即可.
解答:
解:方程
+
=1表示的曲线为C,
对于(1),曲线C,当4-k=k-1>0,解得k=
时,方程表示圆,∴(1)不正确;
对于(2),当1<k<4且k≠
,此时曲线表示椭圆,故(2)不正确;
对于(3),若曲线C表示双曲线,则(4-k)(k-1)<0,可得k<1或k>4,故(3)正确;
对于(4),若曲线C表示焦点在x轴上的椭圆,此时4-k>k-1>0,∴1<k<
,故(4)正确;
故答案为:(3)(4).
| x2 |
| 4-k |
| y2 |
| k-1 |
对于(1),曲线C,当4-k=k-1>0,解得k=
| 5 |
| 2 |
对于(2),当1<k<4且k≠
| 5 |
| 2 |
对于(3),若曲线C表示双曲线,则(4-k)(k-1)<0,可得k<1或k>4,故(3)正确;
对于(4),若曲线C表示焦点在x轴上的椭圆,此时4-k>k-1>0,∴1<k<
| 5 |
| 2 |
故答案为:(3)(4).
点评:本题考查椭圆、双曲线的标准方程,考查学生对椭圆、双曲线的标准方程的理解,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
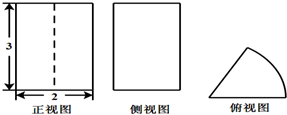 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的侧面积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的侧面积为( )A、12+
| ||
B、6+
| ||
| C、12+2π | ||
| D、6+4π |
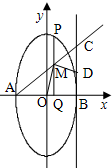 已知椭圆:
已知椭圆: 已知椭圆C的中点在原点,焦点在x轴上,离心率等于
已知椭圆C的中点在原点,焦点在x轴上,离心率等于 已知直线l:y=2x与抛物线C:y=
已知直线l:y=2x与抛物线C:y=