��Ŀ����
��ij��ѧ���˵��������������У�������ʷרҵ�Ŀ����μ������Ļ���ѧ�ƿ��Կ�Ŀ�����ġ��͡���ѧ���Ŀ��ԣ�ij�������������ƿ��Գɼ�����ͳ����ͼ��ʾ�����ο����гɼ���[90��100]�ڵļ�ΪA�����С����ġ���Ŀ�ɼ���[80��90���ڵĿ�����10�ˣ�

������ÿ���������ѧ��Ŀ�ɼ�ΪA��������
������֪�μӱ��������ԵĿ����У�ǡ��2�˵����Ƴɼ���ΪA��������һ�Ƴɼ�ΪA�Ŀ����У������ȡ2�˽��з�̸������2�˵����Ƴɼ���ΪA�ĸ��ʣ�

������ÿ���������ѧ��Ŀ�ɼ�ΪA��������
������֪�μӱ��������ԵĿ����У�ǡ��2�˵����Ƴɼ���ΪA��������һ�Ƴɼ�ΪA�Ŀ����У������ȡ2�˽��з�̸������2�˵����Ƴɼ���ΪA�ĸ��ʣ�
���㣺�ŵ���ͼ�����ʼ��㹫ʽ,Ƶ�ʷֲ�ֱ��ͼ
ר�⣺������ͳ��
�����������ݡ����ġ��͡���ѧ������������ȣ������������=Ƶ����Ƶ�ʵó��ÿ�������������������Ƶ�ʺ�Ϊ1����ȼ�ΪA��Ƶ�ʣ��Ӷ��õ��ÿ��������С���ѧ����Ŀ�гɼ��ȼ�ΪA��������
����ͨ���оٵķ��������ѡ����2�����п��ܵ�����������˵����Ƴɼ��ȼ���ΪA����������ùŵ�����ʹ�ʽ��������ȡ���˽��з�̸�������˵����Ƴɼ��ȼ���ΪA�ĸ��ʣ�
����ͨ���оٵķ��������ѡ����2�����п��ܵ�����������˵����Ƴɼ��ȼ���ΪA����������ùŵ�����ʹ�ʽ��������ȡ���˽��з�̸�������˵����Ƴɼ��ȼ���ΪA�ĸ��ʣ�
���
�⣺���ÿ����Ŀ�������Ϊ10��0.25=40�ˣ�
��ѧ��Ŀ�ɼ�ΪA������Ϊ40����1-0.0025��10-0.015��10-0.0375��10��2��=40��0.075=3�ˣ�
�������ĺ���ѧ�ɼ�ΪA�ĸ���3�ˣ�
���������˵����Ƴɼ���ΪA��
�������ͬѧֻ��һ�Ƴɼ�ΪA��
��������Ϊ�ס��ҡ���������
���мס��ҵ����Ƴɼ���ΪA��
��������һ�Ƴɼ�ΪA�Ŀ����У�
�����ȡ���˽��з�̸��
�����¼�Ϊ{�ף���}��{�ף���}��{�ף���}��{�ң���}��{�ң���}��{������}��6����
�衰�����ȡ���ˣ������˵����Ƴɼ���ΪA��Ϊ�¼�M��
���¼�M�������¼���1����
��P(M)=
��
��ѧ��Ŀ�ɼ�ΪA������Ϊ40����1-0.0025��10-0.015��10-0.0375��10��2��=40��0.075=3�ˣ�
�������ĺ���ѧ�ɼ�ΪA�ĸ���3�ˣ�
���������˵����Ƴɼ���ΪA��
�������ͬѧֻ��һ�Ƴɼ�ΪA��
��������Ϊ�ס��ҡ���������
���мס��ҵ����Ƴɼ���ΪA��
��������һ�Ƴɼ�ΪA�Ŀ����У�
�����ȡ���˽��з�̸��
�����¼�Ϊ{�ף���}��{�ף���}��{�ף���}��{�ң���}��{�ң���}��{������}��6����
�衰�����ȡ���ˣ������˵����Ƴɼ���ΪA��Ϊ�¼�M��
���¼�M�������¼���1����
��P(M)=
| 1 |
| 6 |
��������С����Ҫ����ͳ������ʵ����֪ʶ�������漰��Ƶ�ʷֲ�ֱ��ͼ���ŵ���͵����ݣ����ڻ����⣮

��ϰ��ϵ�д�
�����Ŀ
�������⣺
��1������y=
+x(x��0)��ֵ���ǣ�-�ޣ�-2]��
��2������y=x2+2+
��Сֵ��2��
��3����a��bͬ����a��b����
+
��2��
������ȷ�������ǣ�������
��1������y=
| 1 |
| x |
��2������y=x2+2+
| 1 |
| x2+2 |
��3����a��bͬ����a��b����
| a |
| b |
| b |
| a |
������ȷ�������ǣ�������
| A����1����2����3�� |
| B����1����2�� |
| C����2����3�� |
| D����1����3�� |
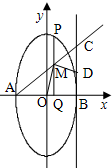 ��֪��Բ��
��֪��Բ��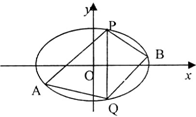 ��֪��ԲC���е���ԭ�㣬������x���ϣ������ʵ���
��֪��ԲC���е���ԭ�㣬������x���ϣ������ʵ��� ��ֱ֪��l��y=2x��������C��y=
��ֱ֪��l��y=2x��������C��y=