题目内容
已知椭圆C:
+
=1(a>b>0)的离心率与等轴双曲线的离心率互为倒数,直线l:x-y+
=0与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
(1)求椭圆C的方程;
(2)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=2,证明:直线AB过定点(-1,-1).
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(1)求椭圆C的方程;
(2)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=2,证明:直线AB过定点(-1,-1).
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件得到e=
,b=
=1,由此能求出椭圆C的方程.
(2)当直线AB的斜率不存在时,设A(x0,y0),则B(x0,-y0),由已知条件推导出x0=-1;当直线AB的斜率存在时,设AB的方程为y=kx+b(b≠1),A(x1,y1),B(x2,y2),由
,得(1+2k2)x2+4kbx+2b2-2=0,利用韦达定理结合已知条件能证明直线AB过定点(-1,-1).
| ||
| 2 |
| ||
|
(2)当直线AB的斜率不存在时,设A(x0,y0),则B(x0,-y0),由已知条件推导出x0=-1;当直线AB的斜率存在时,设AB的方程为y=kx+b(b≠1),A(x1,y1),B(x2,y2),由
|
解答:
(1)解:∵椭圆C:
+
=1(a>b>0)的离心率与等轴双曲线的离心率互为倒数,
∴e=
,
∵直线l:x-y+
=0与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,
∴b=
=1…..(2分)
∴
=
,a2-c2=1,解得a=
…(4分)
∴椭圆C的方程为
2+y2=1…(5分)
(2)证明:当直线AB的斜率不存在时,
设A(x0,y0),则B(x0,-y0),
由k1+k2=2得
+
=2,解得x0=-1….(7分)
当直线AB的斜率存在时,
设AB的方程为y=kx+b(b≠1),A(x1,y1),B(x2,y2),
,整理,得:(1+2k2)x2+4kbx+2b2-2=0,
∴x1+x2=
,x1•x2=
….(9分)
∵k1+k2=2,∴
+
=2,
∴
=2,
即(2-2k)x2x1=(b-1)(x2+x1)⇒(2-2k)(2b2-2)=(b-1)(-4kb)
由b≠1,(1-k)(b+1)=-kb,得k=b+1,…..(11分)
即y=kx+b=(b+1)x+b,∴b(x+1)=y-x
∴直线AB过定点(-1,-1).…..(13分)
| x2 |
| a2 |
| y2 |
| b2 |
∴e=
| ||
| 2 |
∵直线l:x-y+
| 2 |
∴b=
| ||
|
∴
| c |
| a |
| ||
|
| 2 |
∴椭圆C的方程为
| x |
| 2 |
(2)证明:当直线AB的斜率不存在时,
设A(x0,y0),则B(x0,-y0),
由k1+k2=2得
| y0-1 |
| x 0 |
| -y0-1 |
| x 0 |
当直线AB的斜率存在时,
设AB的方程为y=kx+b(b≠1),A(x1,y1),B(x2,y2),
|
∴x1+x2=
| -4kb |
| 1+2k2 |
| 2b2-2 |
| 1+2k2 |
∵k1+k2=2,∴
| y1-1 |
| x1 |
| y2-2 |
| x2 |
∴
| (kx2+b-1)+(kx1+b-1)x2 |
| x1x2 |
即(2-2k)x2x1=(b-1)(x2+x1)⇒(2-2k)(2b2-2)=(b-1)(-4kb)
由b≠1,(1-k)(b+1)=-kb,得k=b+1,…..(11分)
即y=kx+b=(b+1)x+b,∴b(x+1)=y-x
∴直线AB过定点(-1,-1).…..(13分)
点评:本题考查椭圆方程的求法,考查直线过定点的证明,解题时要认真审题,注意分类讨论思想、函数方程思想的合理运用.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
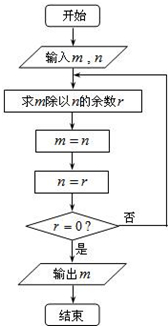 如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的值为( )
如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的值为( )| A、2010 | B、1541 |
| C、134 | D、67 |
设a∈R,则“a=-2”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
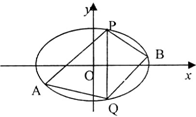 已知椭圆C的中点在原点,焦点在x轴上,离心率等于
已知椭圆C的中点在原点,焦点在x轴上,离心率等于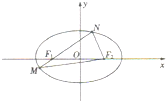 如图,椭圆E:
如图,椭圆E: