题目内容
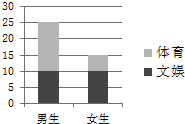 对某班学生是更喜欢体育还是更喜欢文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.
对某班学生是更喜欢体育还是更喜欢文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.(Ⅰ)根据图中数据,制作2×2列联表;
(Ⅱ)若要从更爱好文娱和从更爱好体育的学生中各选一人分别做文体活动协调人,求选出的两人恰好是一男一女的概率;
(Ⅲ)在多大程度上可以认为性别与是否更喜欢体育有关系?参考公式Χ2=
| n(ad-bc)2 |
| (a+c)(b+d)(a+b)(c+d) |
参考数据:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
考点:独立性检验的应用
专题:概率与统计
分析:(1)求出更爱好体育,更爱好文娱,的男生,女生,制作图表,
(2)分两类求解即可得出规概率的求解.
(3)根据公式求解出系数K2,即可运用表格判断.
(2)分两类求解即可得出规概率的求解.
(3)根据公式求解出系数K2,即可运用表格判断.
解答:
解:(Ⅰ)
(Ⅱ)恰好是一男一女的概率是:
=
,
(Ⅲ)K2=
=
=
=2.6666…>2.072
而P(K2>2.072)=0.15
∴有85%的把握可以认为性别与是否更喜欢体育有关系.
| 更 爱 好 体 育 | 更 爱 好 文 娱 | 合 计 | |
| 男 生 | 15 | 10 | 25 |
| 女 生 | 5 | 10 | 15 |
| 合 计 | 20 | 20 | 40 |
| 15×10+5×10 |
| 20×20 |
| 1 |
| 2 |
(Ⅲ)K2=
| n(ac-bd)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 40×(15×10-5×10)2 |
| (15+10)(5+10)(15+5)(10+10) |
| 8 |
| 3 |
而P(K2>2.072)=0.15
∴有85%的把握可以认为性别与是否更喜欢体育有关系.
点评:本题考查了独立检验的思想的运用,属于中档题,计算要准确,认真.

练习册系列答案
相关题目
已知数列
cos0,
cos
,
cosπ,…,
cos
,…,则该数列的所有项之和为( )
| 1 |
| 3 |
| 1 |
| 32 |
| π |
| 2 |
| 1 |
| 33 |
| 1 |
| 3n |
| (n-1)π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
| ∫ |
0 |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}的前n项和为Sn=kn2,若对所有的n∈N*,都有an+1>an,则实数k的取值范围是( )
| A、k<0 | B、k<1 |
| C、k>1 | D、k>0 |
 一流的高尔夫选手约70杆即可打完十八洞,而初学者约160杆才可打完十八洞.如图是甲、乙两位高尔夫选手在五次训练测试中打出的杆数的茎叶图,则发挥比较稳定的选手的方差为
一流的高尔夫选手约70杆即可打完十八洞,而初学者约160杆才可打完十八洞.如图是甲、乙两位高尔夫选手在五次训练测试中打出的杆数的茎叶图,则发挥比较稳定的选手的方差为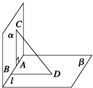 如图所示,在直二面角α-l-β中,A,B∈l,AC?α,AC⊥l,BD?β,BD⊥l,|AC|=6,|AB|=8,|BD|=24,则线段CD的长是( )
如图所示,在直二面角α-l-β中,A,B∈l,AC?α,AC⊥l,BD?β,BD⊥l,|AC|=6,|AB|=8,|BD|=24,则线段CD的长是( )