题目内容
已知矩阵M=
,试求:
(Ⅰ)矩阵M的逆矩阵M-1;
(Ⅱ)直线y=2x在矩阵M-1对应的变换作用下的曲线方程.
|
(Ⅰ)矩阵M的逆矩阵M-1;
(Ⅱ)直线y=2x在矩阵M-1对应的变换作用下的曲线方程.
考点:几种特殊的矩阵变换
专题:矩阵和变换
分析:(Ⅰ)根据定义直接计算;
(Ⅱ)由(Ⅰ)直接计算即可.
(Ⅱ)由(Ⅰ)直接计算即可.
解答:
解:(Ⅰ)∵矩阵M=
,
∴矩阵M的逆矩阵M-1=
;
(Ⅱ)设点P(x,y)是曲线y=2x上任意一点,在矩阵M-1对应的变换作用下得到的点为Q(x',y'),
则
=
=
,
所以
,即
且点P在直线y=2x上,于是得2y′=2×
x′,2y′=x′,
即直线y=2x在矩阵M-1对应的变换作用下的曲线方程为y=
x.
|
∴矩阵M的逆矩阵M-1=
|
(Ⅱ)设点P(x,y)是曲线y=2x上任意一点,在矩阵M-1对应的变换作用下得到的点为Q(x',y'),
则
|
|
|
|
所以
|
|
且点P在直线y=2x上,于是得2y′=2×
| 1 |
| 2 |
即直线y=2x在矩阵M-1对应的变换作用下的曲线方程为y=
| 1 |
| 2 |
点评:本题考查求矩阵的逆矩阵、矩阵与变换等基础知识与运算求解能力,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
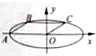 如图,在平面直角坐标系xOy中,点A位椭圆E:
如图,在平面直角坐标系xOy中,点A位椭圆E: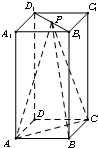 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,P为线段B1D1上一点.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,P为线段B1D1上一点.