题目内容
设F1、F2为椭圆C:
+
=1(a>b>0)的左、右焦点,直线l过焦点F2且与椭圆交于A,B两点,若△ABF1构成以A为直角顶点的等腰直角三角形,设椭圆离心率为e,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、2-
| ||
B、3-
| ||
C、11-6
| ||
D、9-6
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:可设|F1F2|=2c,|AF1|=m,若△ABF1构成以A为直角顶点的等腰直角三角形,则|AB|=|AF1|=m,|BF1|=
m,再由椭圆的定义和周长的求法,可得m,再由勾股定理,可得a,c的方程,运用离心率公式计算即可得到.
| 2 |
解答:
解:可设|F1F2|=2c,|AF1|=m,
若△ABF1构成以A为直角顶点的等腰直角三角形,
则|AB|=|AF1|=m,|BF1|=
m,
由椭圆的定义可得△ABF1的周长为4a,
即有4a=2m+
m,即m=2(2-
)a,
则|AF2|=2a-m=(2
-2)a,
在直角三角形AF1F2中,
|F1F2|2=|AF1|2+|AF2|2,
即4c2=4(2-
)2a2+4(
-1)2a2,
即有c2=(9-6
)a2,
即有e2=
=9-6
.
故选D.
若△ABF1构成以A为直角顶点的等腰直角三角形,
则|AB|=|AF1|=m,|BF1|=
| 2 |
由椭圆的定义可得△ABF1的周长为4a,
即有4a=2m+
| 2 |
| 2 |
则|AF2|=2a-m=(2
| 2 |
在直角三角形AF1F2中,
|F1F2|2=|AF1|2+|AF2|2,
即4c2=4(2-
| 2 |
| 2 |
即有c2=(9-6
| 2 |
即有e2=
| c2 |
| a2 |
| 2 |
故选D.
点评:本题考查椭圆的定义、方程和性质,主要考查离心率的求法,同时考查勾股定理的运用,灵活运用椭圆的定义是解题的关键.

练习册系列答案
相关题目
已知集合S={x|3x+a=0},如果1∈S,那么a的值为( )
| A、-3 | B、-1 | C、1 | D、3 |
圆锥的轴截面是等腰直角三角形,侧面积是16
π,则圆锥的体积是( )
| 2 |
A、
| ||
B、
| ||
| C、64π | ||
D、128
|
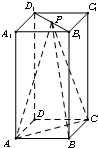 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,P为线段B1D1上一点.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,P为线段B1D1上一点.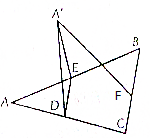 如图所示,在平面α内有一边长为a的等边△ABC,在△ABC中,DE∥BC,沿DE将△ABC折起,使它和△ABC所在半平面成60°的二面角,问直线DE取在何处,折起后的三角形顶点A(可记A′)到BC边的距离最短,最短距离是多少?
如图所示,在平面α内有一边长为a的等边△ABC,在△ABC中,DE∥BC,沿DE将△ABC折起,使它和△ABC所在半平面成60°的二面角,问直线DE取在何处,折起后的三角形顶点A(可记A′)到BC边的距离最短,最短距离是多少?