题目内容
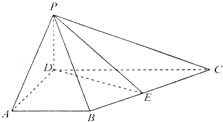 如图,ABCD为梯形,PD⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=
如图,ABCD为梯形,PD⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=| 3 |
| 3 |
(Ⅰ)求证:平面PBC⊥平面PDE;
(Ⅱ)线段PC上是否存在一点F,使PA∥平面BDF?若有,请找出具体位置,并进行证明;若无,请分析说明理由.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)连结BD,由已知得BC⊥DE,BC⊥PD,从而BC⊥平面PDE,由此能证明平面PBC⊥平面PDE.
(Ⅱ)连结AC,BD交于O点,AB∥CD,从而△AOB∽△COD,AB=
DC,进而△CPA中,AO=
AC,由PF=
PC,得OF∥PA,由此得到当点F位于PC三分之一分点(靠近P点)时,PA∥平面BDF.
(Ⅱ)连结AC,BD交于O点,AB∥CD,从而△AOB∽△COD,AB=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
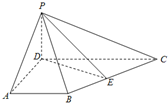 (本小题满分12分)
(本小题满分12分)
(Ⅰ)证明:连结BD,∠BAD=∠ADC=90°,AB=a,DA=
a,
所以BD=DC=2a,E为BC中点,
所以BC⊥DE,…(3分)
又因为PD⊥平面ABCD,所以BC⊥PD,
因为DE∩PD=D,…(4分),所以BC⊥平面PDE,…(5分)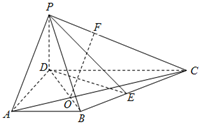
因为BC?平面PBC,所以平面PBC⊥平面PDE.…(6分)
(Ⅱ)解:当点F位于PC三分之一分点(靠近P点)时,
PA∥平面BDF,…(7分)
连结AC,BD交于O点,AB∥CD,所以△AOB∽△COD,AB=
DC,
所以△CPA中,AO=
AC,…(10分)
而PF=
PC,所以OF∥PA,…(11分)
而OF?平面BDF,PA?平面BDF,
所以PA∥平面BDF.…(12分)
 (本小题满分12分)
(本小题满分12分)(Ⅰ)证明:连结BD,∠BAD=∠ADC=90°,AB=a,DA=
| 3 |
所以BD=DC=2a,E为BC中点,
所以BC⊥DE,…(3分)
又因为PD⊥平面ABCD,所以BC⊥PD,
因为DE∩PD=D,…(4分),所以BC⊥平面PDE,…(5分)

因为BC?平面PBC,所以平面PBC⊥平面PDE.…(6分)
(Ⅱ)解:当点F位于PC三分之一分点(靠近P点)时,
PA∥平面BDF,…(7分)
连结AC,BD交于O点,AB∥CD,所以△AOB∽△COD,AB=
| 1 |
| 2 |
所以△CPA中,AO=
| 1 |
| 3 |
而PF=
| 1 |
| 3 |
而OF?平面BDF,PA?平面BDF,
所以PA∥平面BDF.…(12分)
点评:本题考查面面垂直的证明,考查线面平行时点的位置的确定与证明,考查学生的空间想象能力、逻辑推理能力和运算求解能力,是中档题.

练习册系列答案
相关题目
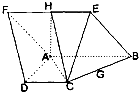 如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点.
如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点. 如图,在平面直角坐标系xOy中,点A位椭圆E:
如图,在平面直角坐标系xOy中,点A位椭圆E: